Question

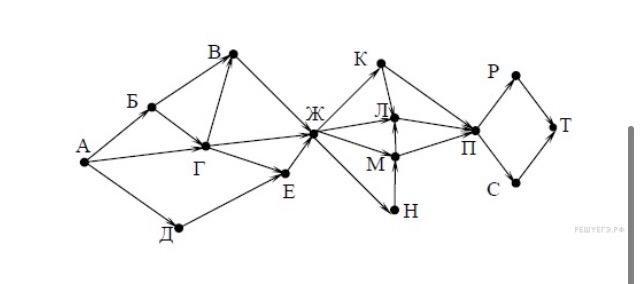
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Ж?

Answer 1

В город М напрямую можно попасть только из города Н (в который напрямую можно попасть только из города Ж), и из города Ж. Значит, для любого пути в Ж из А есть два варианта, как проехать в М.

В город Ж можно попасть напрямую из городов В, Г, и Д. В город В из города А можно попасть тремя путями: АБВ, АГВ и АБГВ, в город Г - двумя: АГ и АБГ, в город Е - тремя: АГЕ, АДЕ и АБГЕ.

Итого: Из города А в город Ж есть 3+2+3=8 путей, из Ж в М - 2 пути. Для каждого пути из А в Ж есть оба варианта пути из Ж в М, поэтому умножаем: 8×2=16 путей.

Ответ: 16 путей

Буду очень благодарен, если Вы отметите мой ответ как лучший!