Найдите объем тела, ограниченного поверхностями, заданными уравнениями
Приложения:

Evgenia4836:
Ответ будет 4, решается через тройной интеграл
Не верно((
Да, извиняюсь это масса, а не объём
Скажите, пожалуйста, а какой верный ответ?
Вы на школьном сайте спрашиваете программу 2-3 курса профильного вуза. Вряд ли кто-то кроме профессоров здесь вам помогут.
Ответы
Ответ дал:
4
- конус второго порядка. В сечении
, параллельном
, будем получать окружность
с центром в начале координат и радиусом
.
- эллиптический параболоид. В сечении
, параллельном
, будем получать окружность
с центром в начале координат и радиусом
.
Найдем кривые пересечения плоскостей:
Вычисление интеграла в приложении.
Приложения:
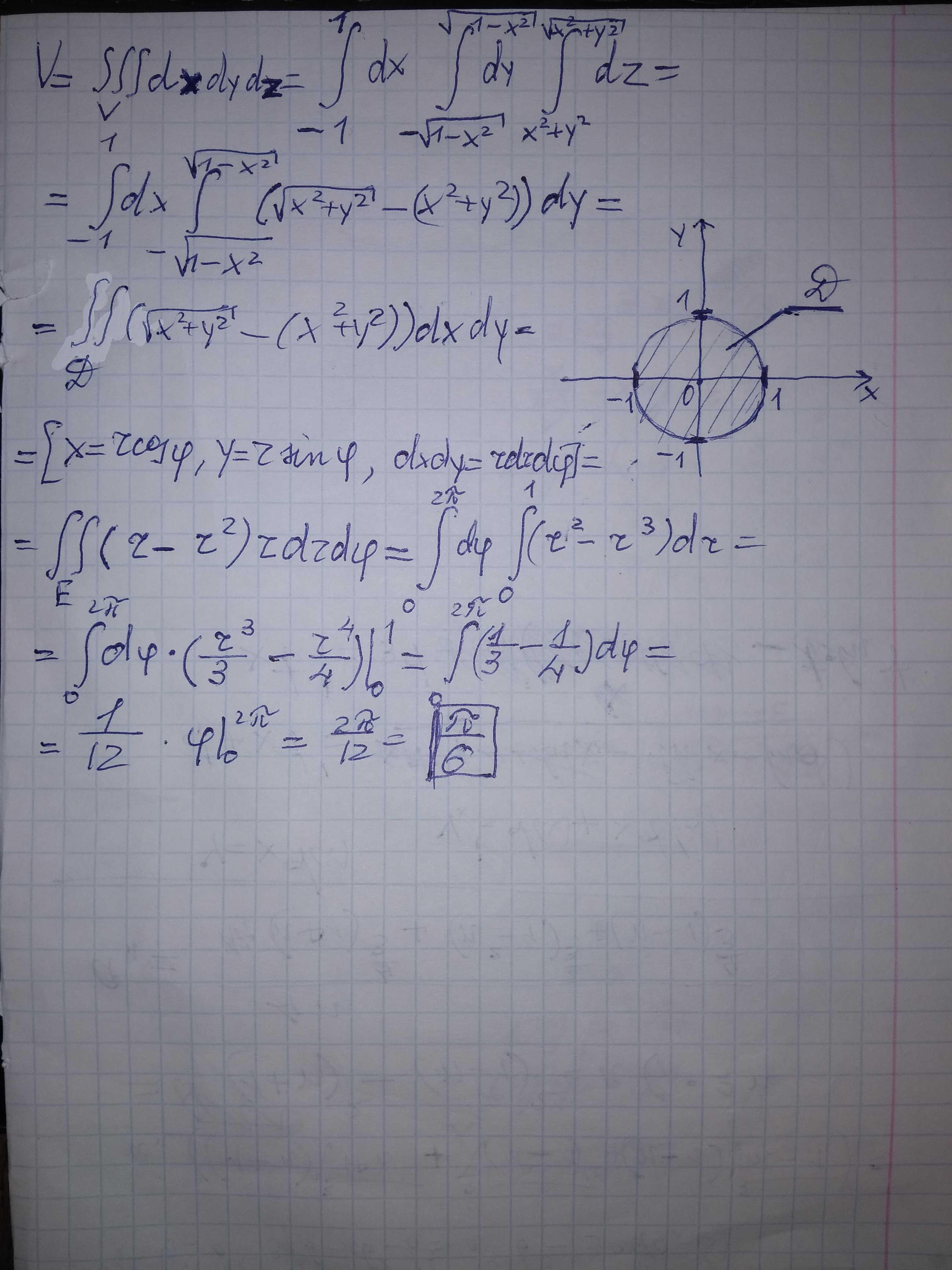
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
8 лет назад