1. В четырехугольнике АВСD проведена диагональ ВD так, что СВD = АDВ, АВD = СDВ. Докажите, что четырехугольник АВСD – параллелограмм. 2. Одна из сторон прямоугольника в 5 раз больше другой, а его периметр равен 36 см. Найдите стороны прямоугольника. 3. Угол между диагональю ромба и его стороной равен 35º. Найти углы ромба. 4. В параллелограмме АВСD биссектриса угла D пересекает сторону АВ в точке Р. Отрезок АР меньше отрезка ВР в 6 раза. Найдите периметр параллелограмма, если АВ = 14 см. 5. Из вершины тупого угла В ромба АВСD опущена высота ВК на сторону AD. Угол КВD равен 15º. Найдите высоту ВК, если периметр ромба равен 32 см. 6. Прямая, пересекающая диагональ ВD параллелограмма АВСD в точке Е, пересекает его стороны АВ и СD в точках М и К соответственно, причем МЕ = КЕ. Докажите, что четырехугольник ВКDМ – параллелограмм.
Ответы
Ответ дал:
1
Ответ:
1.Только там BC//AD надо писать под CBD=ADB
Приложения:
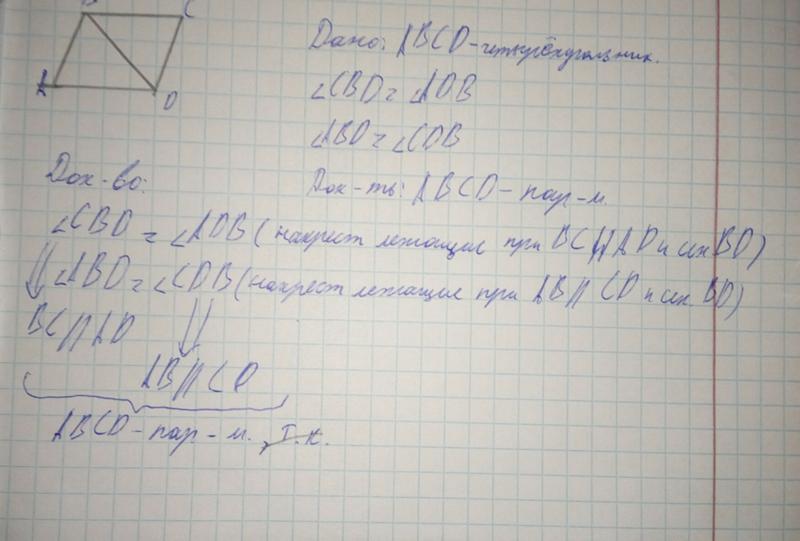
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад