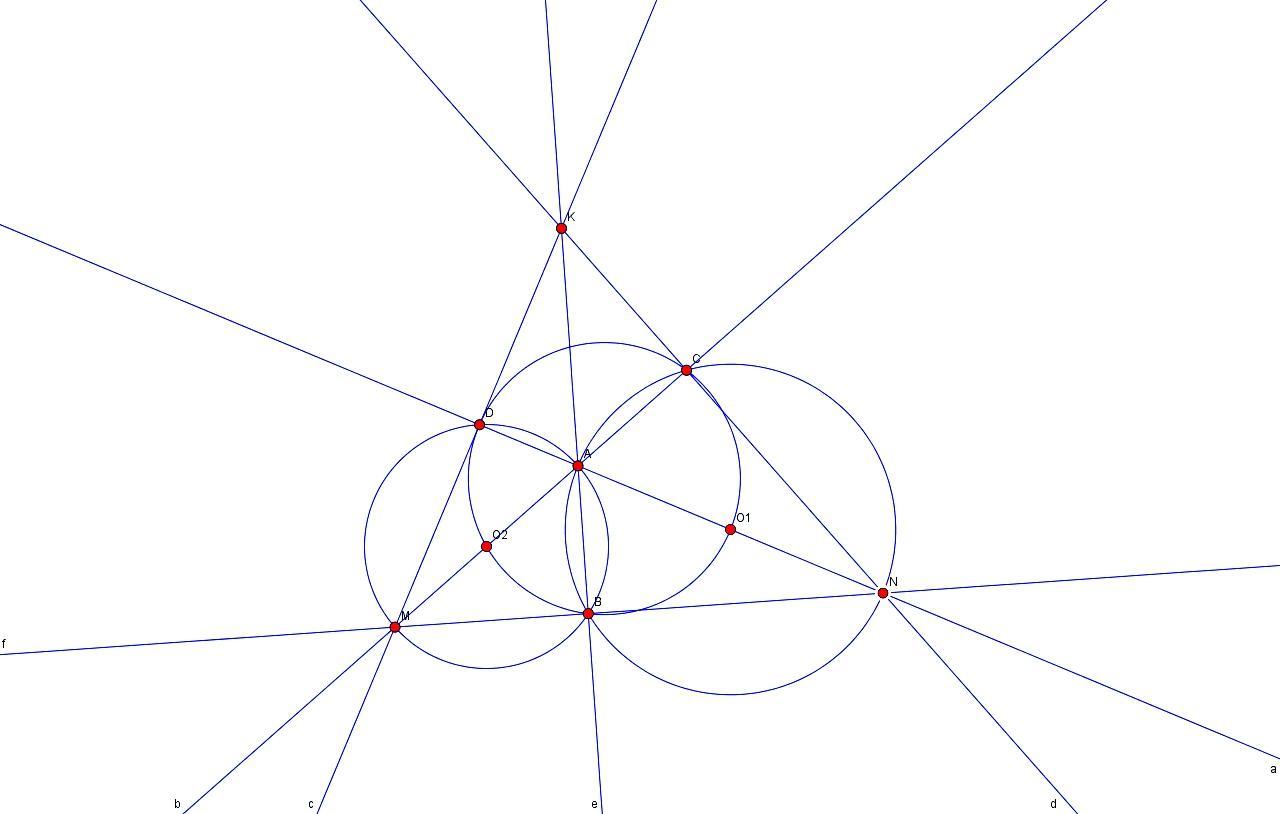
Окружности с центрами O1 и O2 пересекаются в точках A и B. Луч O2A пересекает первую окружность в точке C. Докажите, что точки O1, O2, B, C лежат на одной окружности.
Ответы
См. чертеж.
Если построить точку D как продолжение O1A, также как C лежит на продолжении O2A, а потом провести прямые NC и MD (MA и NA - диаметры), то они пересекутся в какой-то точке K.
Прямые MC и NK перпендикулярны, поскольку угол MCN вписанный и опирается на диаметр. Аналогично перпендикулярны и MK и ND;
Отсюда следует вот что.
Если обозначить угол MKN как K, то
KD = KN*cos(K); и KC = KM*cos(K);
=> KD*KM = KN*KM*cos(K)=KC*KN;
то есть степени точки K относительно обеих окружностей равны, и она обязательно принадлежит радикальной оси AB.
То есть три прямые KN, KM и AB пересекаются в одной точке K.
Если теперь соединить точки M и N c точкой B, то углы MBA и NBA будут прямыми, так как это опять вписанные углы, опирающиеся на диаметры. Поэтому отрезки MB и NB принадлежат одной прямой, перпендикулярной прямой AB (на которой лежит и точка K).
Получился треугольник MNK, в котором A - ортоцентр, O1 и O2 - середины отрезков высот от вершины до ортоцентра MA и NA, а точка B - основание высоты KB.
Отсюда следует, что окружность O1O2B - это окружность Эйлера для MNK. Разумеется, она содержит все основания высот - и С, и D тоже. А еще - середины сторон...
Если кто-то не заметил - уже все кончилось :) Задача решена.