Question

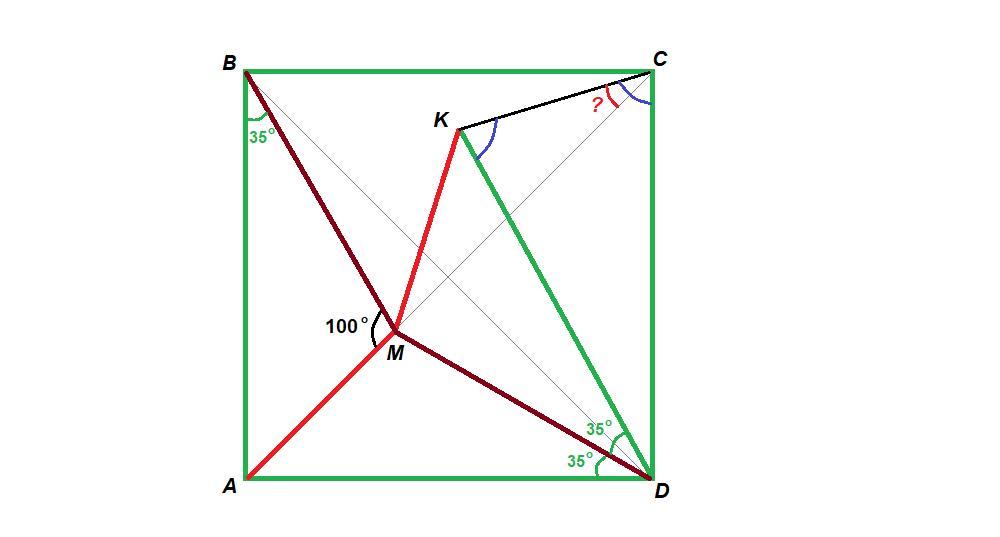
Внутри квадрата ABCD отмечены точки К и М (точка М находит- ся внутри треугольника ABD, точка К - внутри ВМС") так, что треугольники ВАМ и DKM равны (AM = KM, BM = MD, AB = KD), Найдите Угол KCM, если Угол AMB = 100

Answer 1

Ответ:

35°

Объяснение:

По условию BM = DM, а все точки, равноудаленные от концов отрезка BD лежат на серединном перпендикуляре к BD, т.е. на диагонали АС, значит М лежит на АС.

Тогда ∠ВАМ = 45°, а из ΔВАМ

∠АВМ = 180° - (∠АМВ + ∠ВАМ) = 180° - (100° + 45°) = 35°

Из равенства треугольников ВАМ и DKM следует, что

∠KDM = ∠ABM = 35°

По условию АВ = KD, значит

KD = AD = DC.

Тогда ΔADM = ΔKDM по трем сторонам (AD = KD (см. выше), DM - общая, АМ = КМ по условию), значит

∠ADM = ∠KDM = 35°

___

∠KDC = ∠ADC - (∠ADM + ∠KDM) = 90° - (35° + 35°) = 20°

ΔKDC равнобедренный, а значит углы при основании равны:

∠DKC = ∠DCK = (180° - 20°) / 2 = 80°

∠КСМ = ∠DCK - ∠DCA = 80° - 45° = 35°