Question

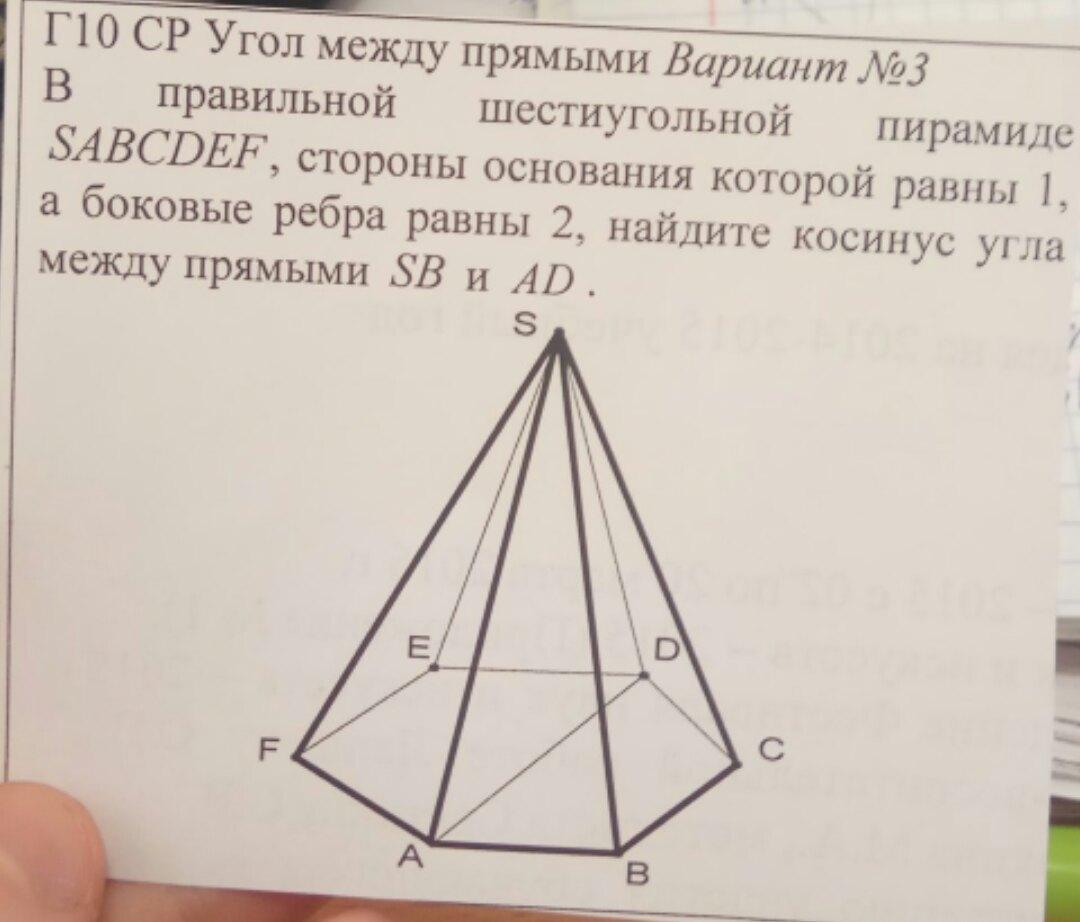
50 баллов. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми sb и ad.

надо очень срочно

Answer 1

Пусть А - начало координат

Ось X - АВ

Ось Y - АЕ

Ось Z - перпендикулярно основанию в сторону S

Пусть высота пирамиды h

Координаты точек

A(0;0;0)

D(1;√3;0)

S(0.5;√3/2;h)

B(1;0;0)

Вектора

AD( 1; √3;0)  Длина 2

SB (0.5;-√3/2;-h)  Длина 2

Косинус искомого угла

| AD * SB | / | AD | / | SB | =

| 1 *0.5-√3*√3/2 | / 2 / 2= 1/4