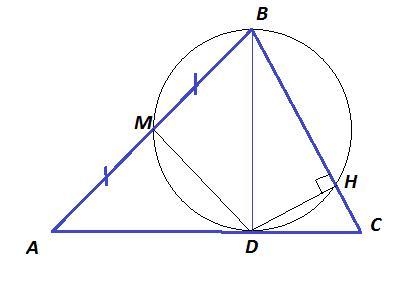
На стороне AC треугольника ABC выбрана точка D. Точка H-основание перпендикуляра, опущенного из точки D на сторону BC. Точка M-середина стороны AB. Известно, что точки B, M, D, H лежат на одной окружности. Докажите, что угол BDC в два раза больше угла BAC.
Ответы
Ответ дал:
3
Дано : DH⊥BC, AM = MB, BMDH - вписанный четырёхугольник.
Доказать : ∠BDC = 2∠BAC
Доказательство :
DH ⊥ BC ⇒ ΔDHB - прямоугольный, вписан в окружность ⇒
гипотенуза треугольника DB - диаметр окружности ⇒
ΔDMB тоже прямоугольный, ∠DMB = 90°
Диаметр окружности в точку касания образует прямой угол с касательной ⇒ ∠ADB = ∠BDC = 90°
ΔADB - прямоугольный, DM - высота и медиана (AM=MB) ⇒
ΔADB равнобедренный ⇒ ∠ABD = ∠BAD = 90° : 2 = 45°
∠BDC = 2∠BAC =2·45° = 90°
Приложения:
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад