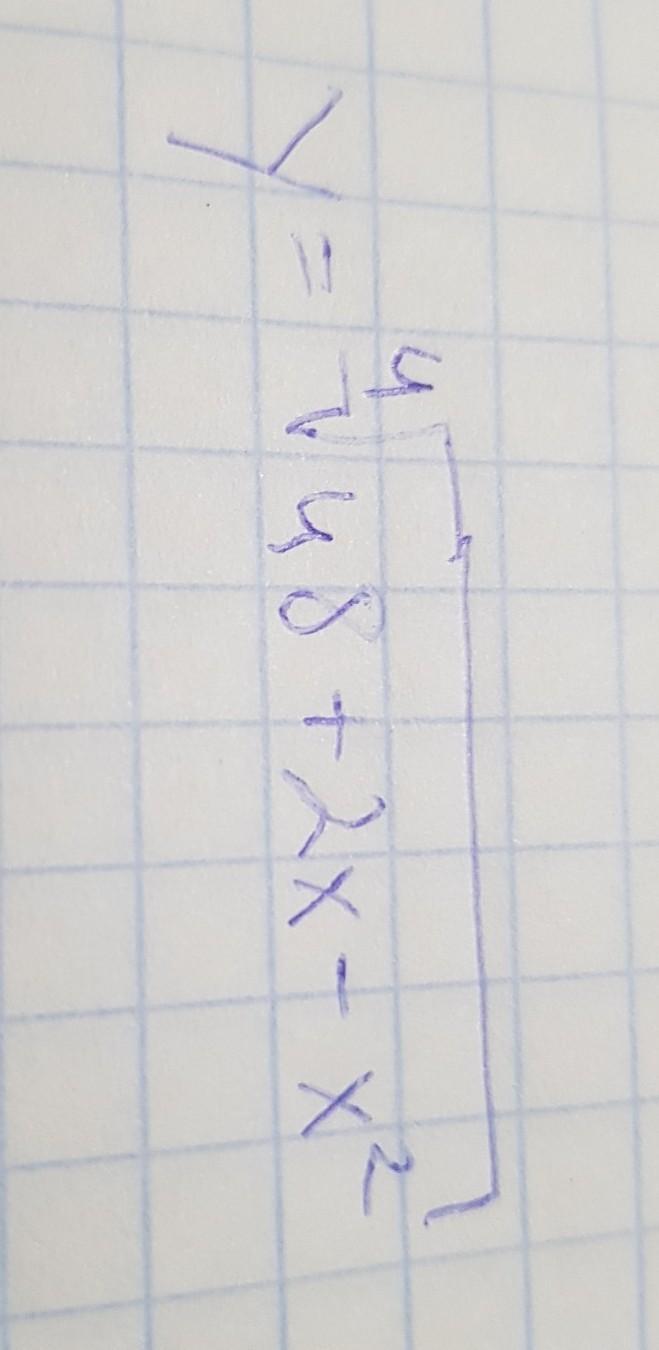Question

Найти область значений​

Answer 1

Ответ:

Пошаговое объяснение:

Найдем область значений 48+2x-x²=-x²+2x+48.

Коэффициент при x² равен -1<0, значит ветви параболы направлены вниз. Наибольшее значение -x²+2x+48 принимает в точке вершины.

Координата x вершины $xv=-\frac{b}{2a}=-\frac{2}{-2}=1$

Значение функции -x²+2x+48 в этой точке равно = -1+2+48=47.

Наибольшее значение -x²+2x+48 равно 47.

Наибольшее значение $\sqrt[4]{-x^2+2x+48}$ равно $\sqrt[4]{47}$.

Область значения $\sqrt[4]{-x^2+2x+48}$: $(0; \sqrt[4]{47})$