Question

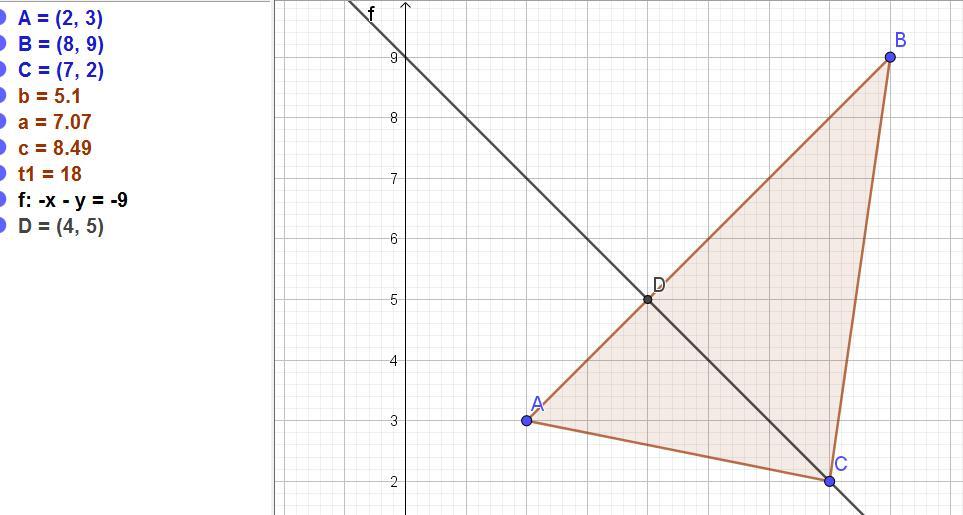
Даны координаты вершин треугольника ABC: A(2;3) B(8;9) C(7;2). Найдите ординату точки высоты CD или её продолжения с прямой x=5

Answer 1

Уравнение прямой, содержащей сторону АВ:

АВ: (х - 2)/6 = (у - 3)/6.   Уравнение АВ: у = х + 1.

Высота СД - это перпендикуляр к АВ. к(СД) = -1/к(АВ) = -1/1 = -1.

Уравнение СД: у = -х + в. Подставим координаты точки С:

2 = -1*7 + в,  отсюда в = 2 + 7 = 9.

Уравнение СД: у = -х + 9.

Точка Д одновременно принадлежит АВ и СД, приравняем уравнения:

х + 1 = -х + 9,

2х = 8,

х = 8/2 = 4.

у = 4 + 1 = 5. Это ответ.