Question

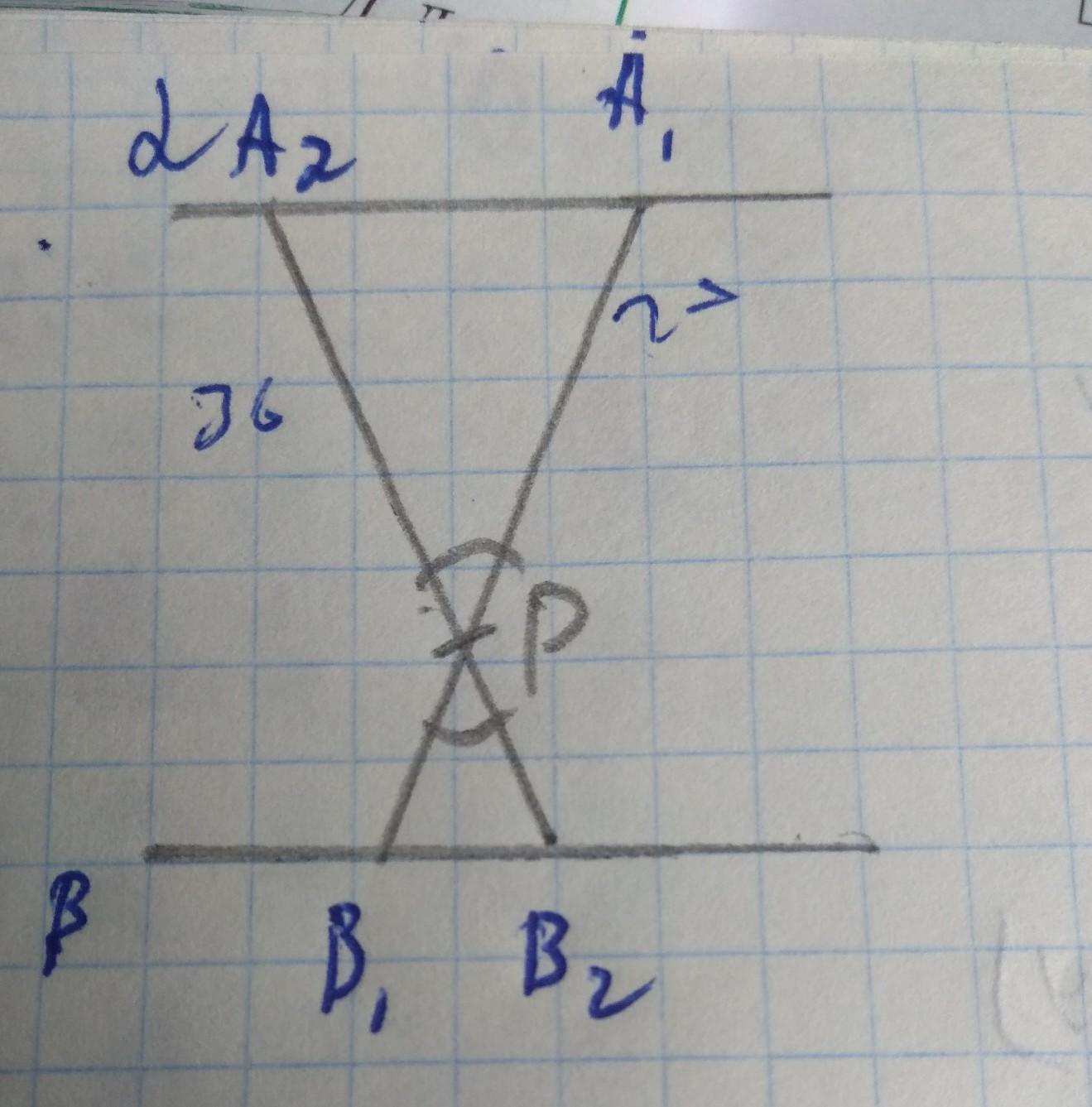
Плоскости альфа и бета параллельны
Прямая а пересекает альфа в точке А1, а пересекает бета в точке В1
b пересекает бета в точке А2, b пересекает бета в точке В2
РА2 : РВ2 = 7 : 2
А1В1=27дм
А2В2=36дм
А1Р-?
А2Р-?
График выше​

Answer 1

1) A2P

РА2 : РВ2 = 7 : 2

Разделим всю прямую на 7+2 = 9 равных частей.

A2P = A2B2 : 9 = 36 : 9 = 4 - значит одна часть будет равна 9

Из этого следует:

A2P = 7 * 4 = 28

2) Докажем подобие треугольников A2A1P и B1PB2:

а) Углы B1PB2 = углу A2PA1, как вертикальные

б) Стороны PA2 и PB2 пропорциальны

в) Углы B1 = A1 , как внутренние пересекающиеся

Следует, что они подобны значит A1P также пропорцианальна к PB1, как 7:2

т.е 27:9=3 - это одна часть

Следует, A1P=3*7=21

Ответ: A1P = 21

           A2P = 28