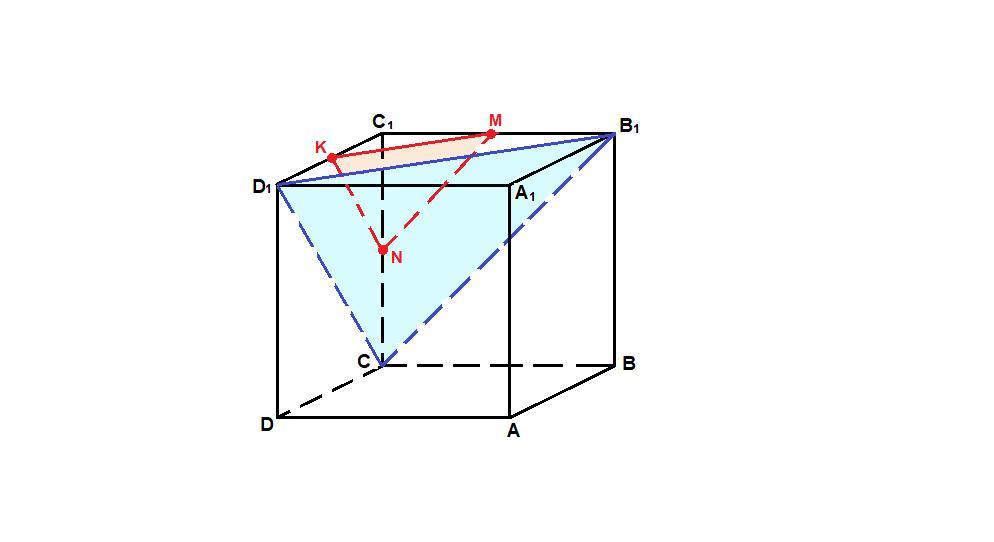
Докажите, что плоскость проведенная через середины ребер Д1С1, В1С1, и СС1 куба АВСДА1В1С1Д1
параллельна плоскости СВ1Д1.
с рисунком, пожалуйста
Ответы
Ответ дал:
15
Ответ:
Пусть К, M и N - середины указанных ребер.
Надо доказать, что плоскость (KMN) параллельна плоскости (CB₁D₁).
Признак параллельности плоскостей:
если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
КМ║B₁D₁ как средняя линия ΔB₁C₁D₁,
KN║D₁C как средняя линия ΔD₁C₁C.
Значит, (KMN)║(CB₁D₁).
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад