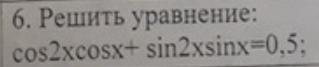Ответы
Ответ дал:
1
Дано уравнение cos(2x)*cos(x) + sin(2x)*sin(x) = 0,5.
Используем формулы двойного аргумента.
(1 - 2sin²(x))*cos(x) + 2sin(x)cos(x)*sin(x) = 0,5.
cos(x) - 2sin²(x)*cos(x) + 2sin²(x)cos(x) = 0,5.
После сокращения получаем cos(x) = 0,5.
Ответ: x = (π/3) + 2πk, k ∈ Z.
x = (-π/3) + 2πk, k ∈ Z.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад