Question

1. Задайте формулой обратно пропорциональную зависимость, если известно, что значению аргумента, равному $frac{1}{7}$, соответствует значение функции, равное 4.
2.решите графически $frac{9}{x}=x$
3. Определите графически, сколько решений имеет уравнение
$frac{1}{x}=2.5-x$

Answer 1

Если это уравнение прямой 
$f(frac{1}{7})=k*frac{1}{7}=4\ k=28\ f(x)=28x\ f(x)=frac{28}{x}$

Графический нужно график нарисовать , левая часть уравнения это гипербола, правая это прямая и очевидно она пересекает гиперболу в двух точках, значит это два корня, 3 и -3 

Слева гипербола , а справа график прямой, и она тоже пересекает данную гиперболу в двух точках , два решения 

Answer 2

Спасибо, а ты бы не мог 3 по подробнее расписать, а то я не могу подставить, чтобы получить гиперболу

Answer 3

1.  Обратно пропорциональная зависимость :

      $y=dfrac kx;~~~~~x=dfrac 17;~~~~y=4\\4=k:dfrac 17~~~~Rightarrow~~~~k=28~~~~Rightarrow~~~~boxed{boldsymbol{y=dfrac{28}x}}$

2. Решите графически     $dfrac 9x=x$

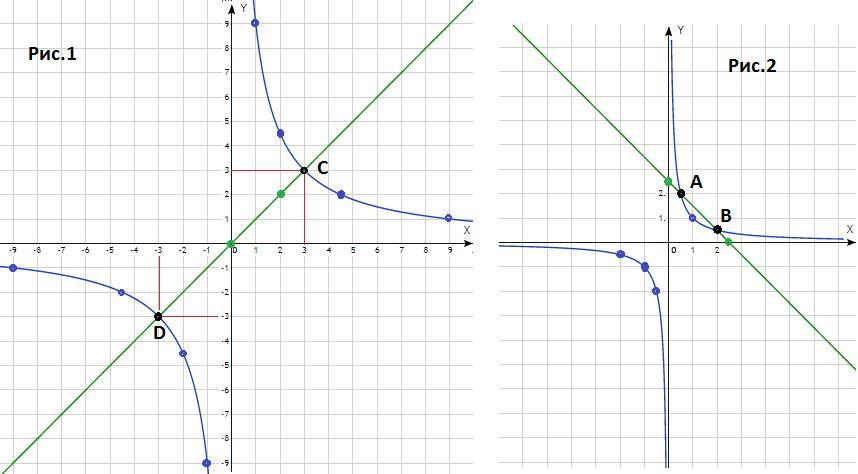
   График функции     $y=dfrac 9x$   -   гипербола в первой и третьей четвертях (k=9>0).  Точки для построения :

x     -9     -4,5     -3     -2      -1      1       2      3     4,5     9

y      -1      -2      -3    -4,5    -9     9     4,5     3       2      1

  График функции   y = x   -   прямая линия, проходящая через начало координат. Точки для построения

x     0      2

y     0      2

  Ответ : (-3; -3)  и  (3; 3)  -  рис. 1.

3. Графически, сколько решений имеет уравнение  $dfrac 1x=2,5-x$

   График функции     $y=dfrac 1x$  -   гипербола в первой и третьей четвертях (k=1>0).  Точки для построения :

x        -2       -1     -0,5     0,5     1       2

y      -0,5      -1      -2         2      1     0,5

  График функции   y = 2,5 - x   -   прямая линия. Точки для построения

x     0       2,5

y     2,5     0

  Ответ : уравнение имеет 2 решения  -  рис. 2.