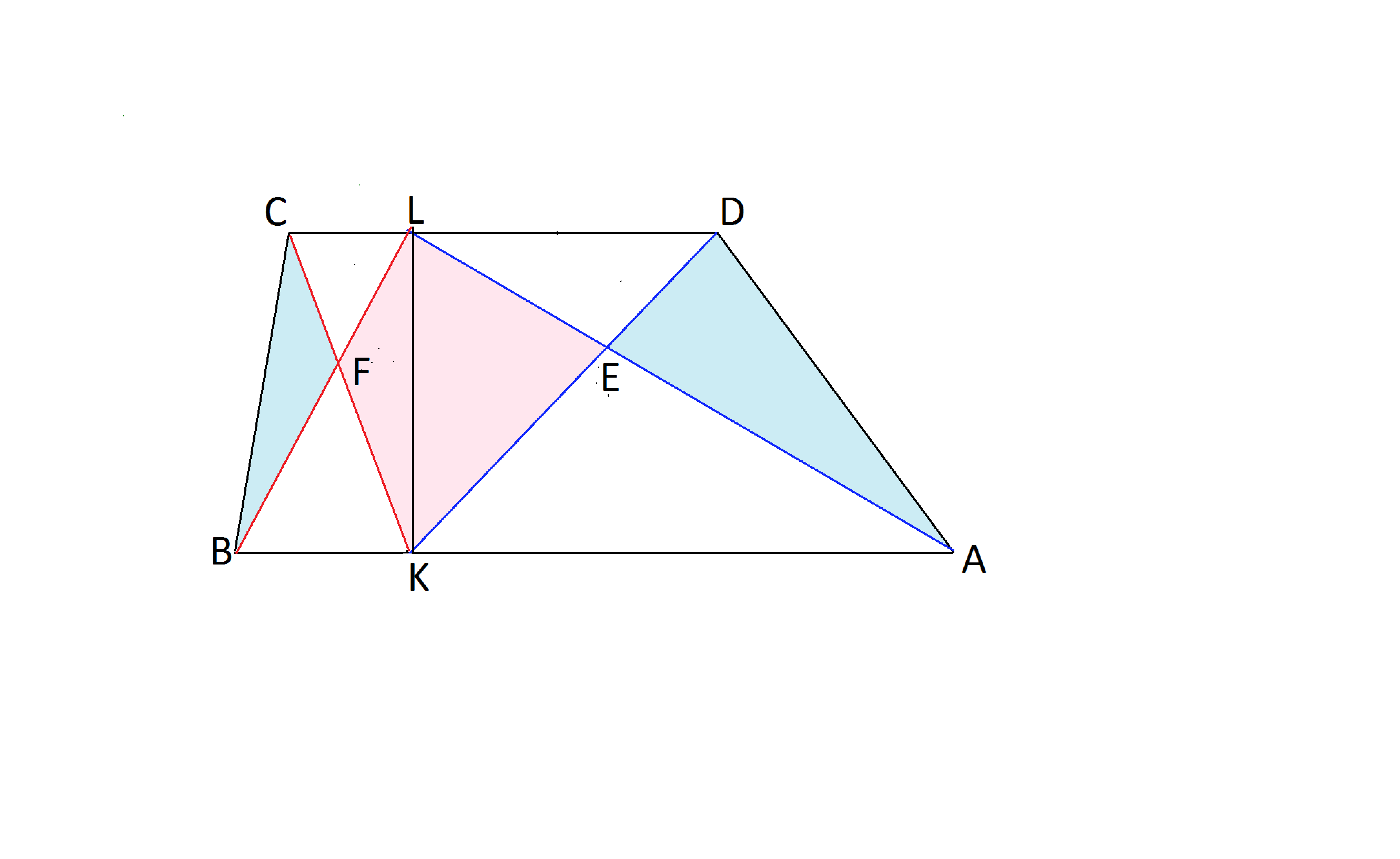
На основаниях АВ и СD трапеции АВСD взяты точки Kи L.
Пусть Е - точка пересечения отрезков AL и DK, F-точка пересечения
BL и CK. Доказать, что сумма площадей треугольников АДЕ и ВСF и равна площади четырехугольника EKFL
Ответы
Ответ дал:
0
Соединив точки L и К, получим две новые трапеции CLKB и LDAK.
Есть такая теорема:
Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь.
Одинаковую площадь имеют треугольники, основаниями которых являются боковые стороны трапеции.
Треугольники ВСF и LКF в трапеции СLКВ равновелики (площади треугольников ВLС и СLК равны по равному основанию СL равной высоте, и треугольник CLF в них общий) Точно так же треугольники LЕК и ЕDА в трапеции LКАD также имеют равную площадь
А так как четырехугольник LЕКF содержит по треугольнику из каждой пары, его площадь равна сумме площадей треугольников АDЕ и ВСF.
Что и требовалось доказать
Есть такая теорема:
Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь.
Одинаковую площадь имеют треугольники, основаниями которых являются боковые стороны трапеции.
Треугольники ВСF и LКF в трапеции СLКВ равновелики (площади треугольников ВLС и СLК равны по равному основанию СL равной высоте, и треугольник CLF в них общий) Точно так же треугольники LЕК и ЕDА в трапеции LКАD также имеют равную площадь
А так как четырехугольник LЕКF содержит по треугольнику из каждой пары, его площадь равна сумме площадей треугольников АDЕ и ВСF.
Что и требовалось доказать
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад