Ответы
Ответ дал:
0
Ответ:
36
Пошаговое объяснение:
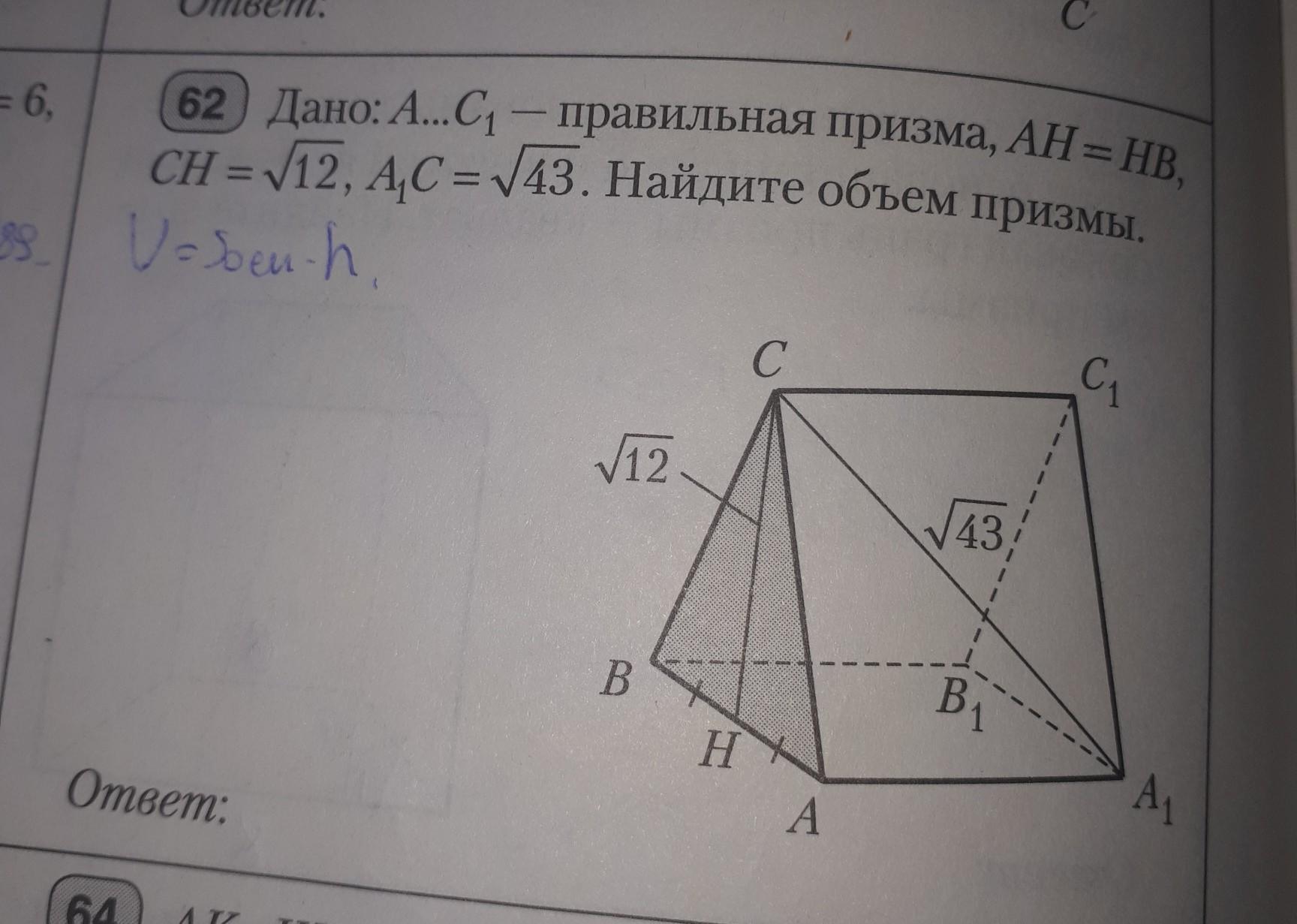
Поскольку призма правильная, то треугольник ABC равносторонний с углами 60°, а СН - высота треугольника АВС
Сторона АС равна СН/sin(∠САВ) = √12 / sin60° = 2*√12/√3 = 2*√4 = 4
Угол прямой, значит по теореме Пифагора для треугольника
Площадь основания АВС равна (СН * АВ) / 2 = √12*4/2 = 4√3
Объем пирамиды равен площадь основания АВС на высоту = 4√3 * 3√3 =12*3=36
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад