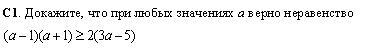Ответы
Ответ дал:
1
Решение задания приложено
Приложения:

matilda17562:
В скобках ошибка. Нужен квадрат разности.
Я заметила
Ответ дал:
1
Доказать, что
(а - 1)(а + 1) ≥ 2•(3а - 5) при любых значениях а.
Доказательство:
Оценим разность
(а - 1)(а + 1) - 2•(3а - 5) = а^2 - 1 - 6а + 10 = а^2 - 6а + 9 = (а - 3)^2 ≥ 0 при всех значениях а,
тогда по определению и (а - 1)(а + 1) ≥ 2•(3а - 5) при любом значении переменной а, ч.т.д.
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад