Question

Помогите! СРОЧНО! ПОЖАЛУЙСТА!
ДАЮ МНОГО БАЛЛОВ!
СВЯЗАННО С ФУНКЦИЯМИ!
ВСЕ 4 ЗАДАНИЯ! ТЕСТЫ!

Answer 1

Ответ:

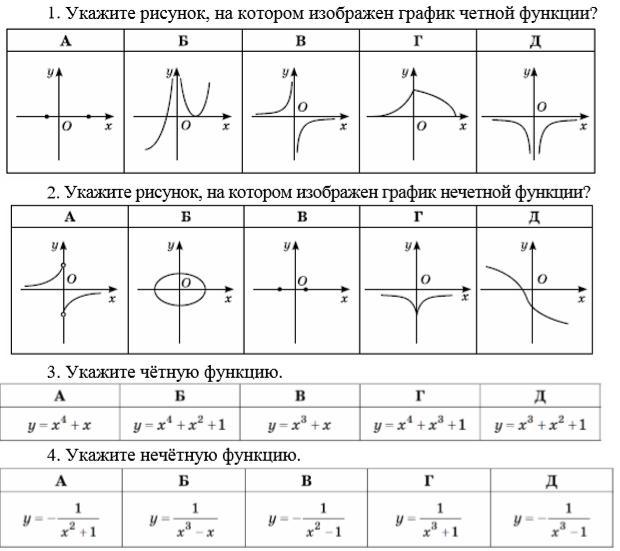
1) Д

2) А

3) Б

4) Б

Объяснение:

Свойства и определения:

Функция четная, когда

f(x) = f(-x)

и нечетна, когда

f(x) = -f(x)

3) у = х^4 + х^2 + 1

у(-х) = (-х)^4 + (-х)^2 + 1 =

= х^4 + х^2 +1 = y(x)

так как (-х)^2n = x^2n для любого целого n

4) y = 1 / (x^3 - x)

y(-x) = 1 / [(-x)^3 - (-x)] =

= 1 / (-x^3 + x) =

= -1 / (x^3 -x) = -y(x)

так как (-х)^(2n+1) = -x^(2n+1) для любого целого n

Answer 2

1)  График любой чётной функции симметричен относительно оси ОУ. То есть, если перегнуть график по оси ОУ, то линия в правой полуплоскости совпадёт с линией в левой полуплоскости. Таким свойством обладает график Д).

2)  График любой нечётной функции симметричен относительно точки О(0,0), начала координат. Это график А).

3)  Чётная функция обладает свойством:   $y(-x)=y(x)$  . Такой функцией является функция  Б), так как

$y=x^4+x^2+1\\\\y(-x)=(-x)^4+(-x)^2+1=x^4+x^2+1=y(x)$

4)  Нечётная  функция обладает свойством:   $y(-x)=-y(x)$  . Такой функцией является функция  Б), так как

$y=\frac{1}{x^3-x}\\\\y(-x)=\frac{1}{(-x)^3-(-x)}=\frac{1}{-x^3+x}=\frac{1}{-(x^3-x)}=-\frac{1}{x^3-x}=-y(x)$