угол между двумя прямыми
Приложения:
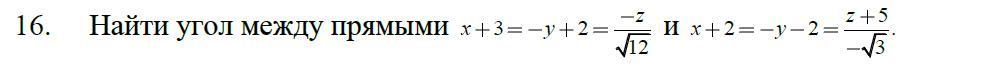
Simba2017:
равен углу между их направляющими векторами
n1(1;-1;-V12) и n2(1;-1;-V3)
V-знак корня
это уже школа...
24 градуса примерно
мог бы скинть решение поподробнее
это не школа?
вышмат
Ответы
Ответ дал:
1
представлю уравнения в каноническом виде
(x+3)/1=(y-2)/(-1)=z/(-√12)-тогда направляющий вектор этой прямой
n1(1;-1;-√12)
у второй (x+2)/1=(y+2)/(-1)=(z+5)/(-√3)
n2(1;-1;-√3)
тогда угол между прямыми равен углу между направляющими векторами. Вычислю его через скалярное произведение этих векторов
В координатах оно равно
(n1,n2)=1*1+(-1)*(-1)+(-√12)*(-√3)=1=1+6=8
оно же (n1,n2)=|n1|*|n2|*cosx
|n1|=√(1+1+3)=√5
|n2|=√(1+1+12)=√14
cosx=(n1,n2)/(|n1|*|n2|)=8/(√5*√14)=8/√70≈0.956
x=arccos 0.956=17 градусов
спасибо ,решал , но забыл домножить на cosx
Помогите пожалуйста мне по математике
помогите пожалуйста мне по математике
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад