Ответы
Ответ дал:
0
В первом использовал второй замечательный предел
Во втором показал что степень стремиться к бесконечности
Приложения:
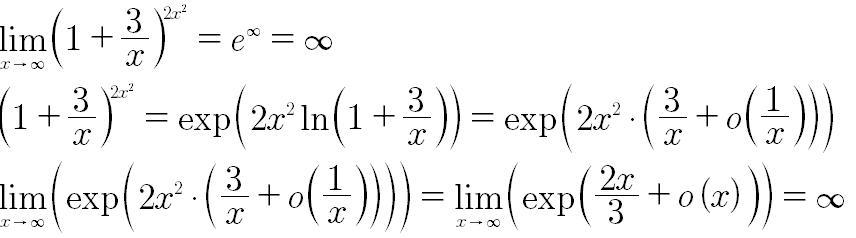
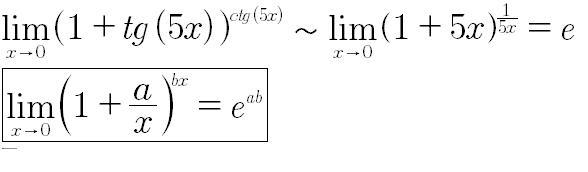
arkadiysudakov00:
По моему тут решен лишь один предел из двух.
Ответ дал:
1
1)
Воспользуемся эквивалентами бесконечно малых:
В итоге получится второй замечательный предел:
2)
Извиняюсь ,я просто слепой
Это у Вас ошибка.
Вам надо было исправить опечатку (2 - x^2) на (2x^2), а вы всё переделали
Вам надо было исправить опечатку (2 - x^2) на (2x^2), а вы всё переделали
Исправил
Это вот выше вы хотите сказать,что полное решение? Мне нужно полное.....
В первом примере вообще не понятно решение.И нету полного.
Второй замечательный предел! Всё предельно ясно написал человек! Прочитайте хотя бы теорию по пределам
Это краткое решение и есть првильный ответ ? Мне надо решить эти пределы не пользуясь правилом Лопиталя с подробным расписанием и решением
Да никто тут не использовал правило Лопиталя! Мне кажется вы просто выучили это слово "Лопиталь" и даже не понимаете ,что оно значит и не видите когда его применяют
Так я и говорю что эти краткие решения и есть правильный ответ ?!
Да!
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
