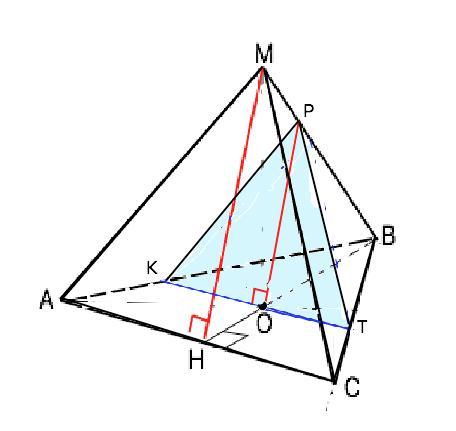
Постройте сечение треугольной пирамиды плоскостью, проходящей через центр основания параллельно боковой грани. Вычислите периметр сечения, если каждое ребро пирамиды равно 2 см.
Ответы
Ответ: 4 см
Объяснение (подробно) :
Обозначим данную пирамиду МАВС. О - центр её основания. Центром основания данной пирамиды - правильного треугольника - является точка пересечения его высот, (биссектрис и медиан)
Для построения нужной плоскости проведем ОР параллельно высоте МН боковой грани АМС, и КТ параллельно ребру АС основания. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, эти плоскости параллельны.
Центр ∆ АВС делит медиану ВН в отношении 2:1, считая от вершины В ( свойство медиан треугольника). Плоскость сечения КРС параллельна ∆ АМС и является треугольником, подобным ему. Коэффициент подобия равен ВК:ВА=ВО:ВН=2:3. Периметр сечения относится к периметру грани АМС как 2:3. Периметр ∆АМС=3•2=6.
Р (КРТ)=6•2/3=4 см