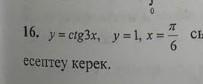Ответы
Ответ дал:
1
Приложения:
Ruuі:
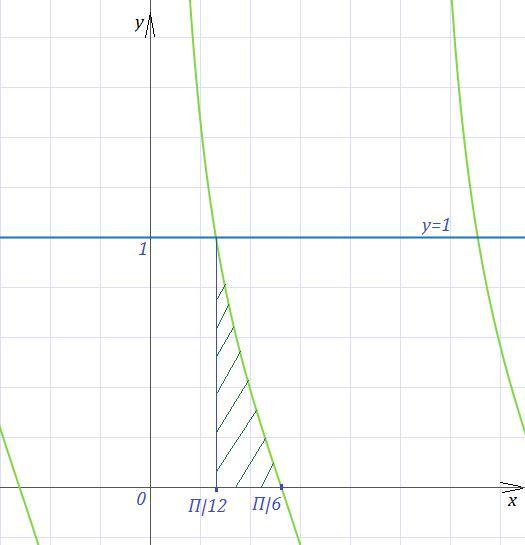
у=х^2,у=х^4 найти площадь фигуры ограниченной линиями
Помогите начертить график
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад