Question

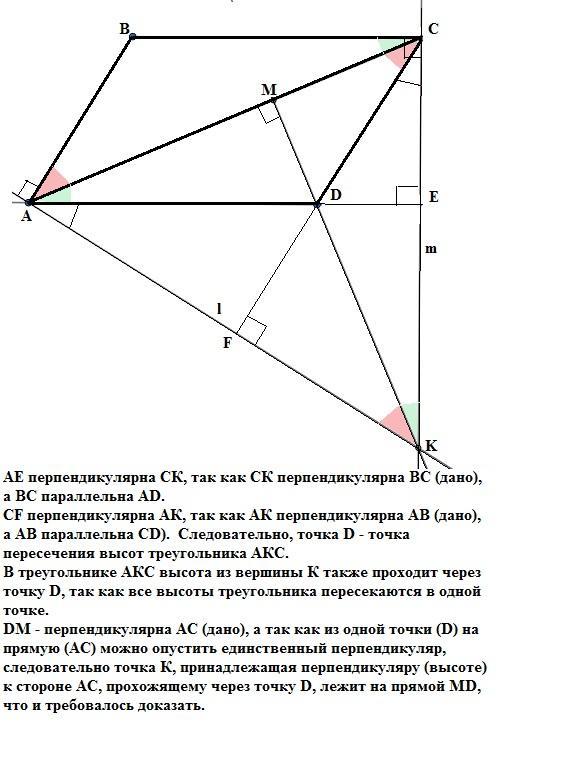
Точка `M` лежит на диагонали AC параллелограмма ABCD, причём DM_|_AC. Прямая `l` проходит через точку `A` и перпендикулярна AB; прямая m проходит через точку C и перпендикулярна BC. Верно ли, что точка пересечения прямых l и m лежит на прямой DM?

Answer 1

Ответ:

Доказательство в объяснении.

Объяснение:

AE перпендикулярна СК, так как СК перпендикулярна BC (дано), а ВС параллельна AD.

CF перпендикулярна AК, так как АК перпендикулярна АВ (дано), а АВ параллельна СD).  Следовательно, точка D - точка пересечения высот треугольника АКС.

В треугольнике АКС высота из вершины К также проходит через точку D, так как все высоты треугольника пересекаются в одной точке.

DM - перпендикулярна АС (дано), а так как из одной точки (D) на прямую (АС) можно опустить единственный перпендикуляр, следовательно точка К, принадлежащая перпендикуляру (высоте) к стороне АС, прохожящему через точку D, лежит на прямой MD, что и требовалось доказать.