Question

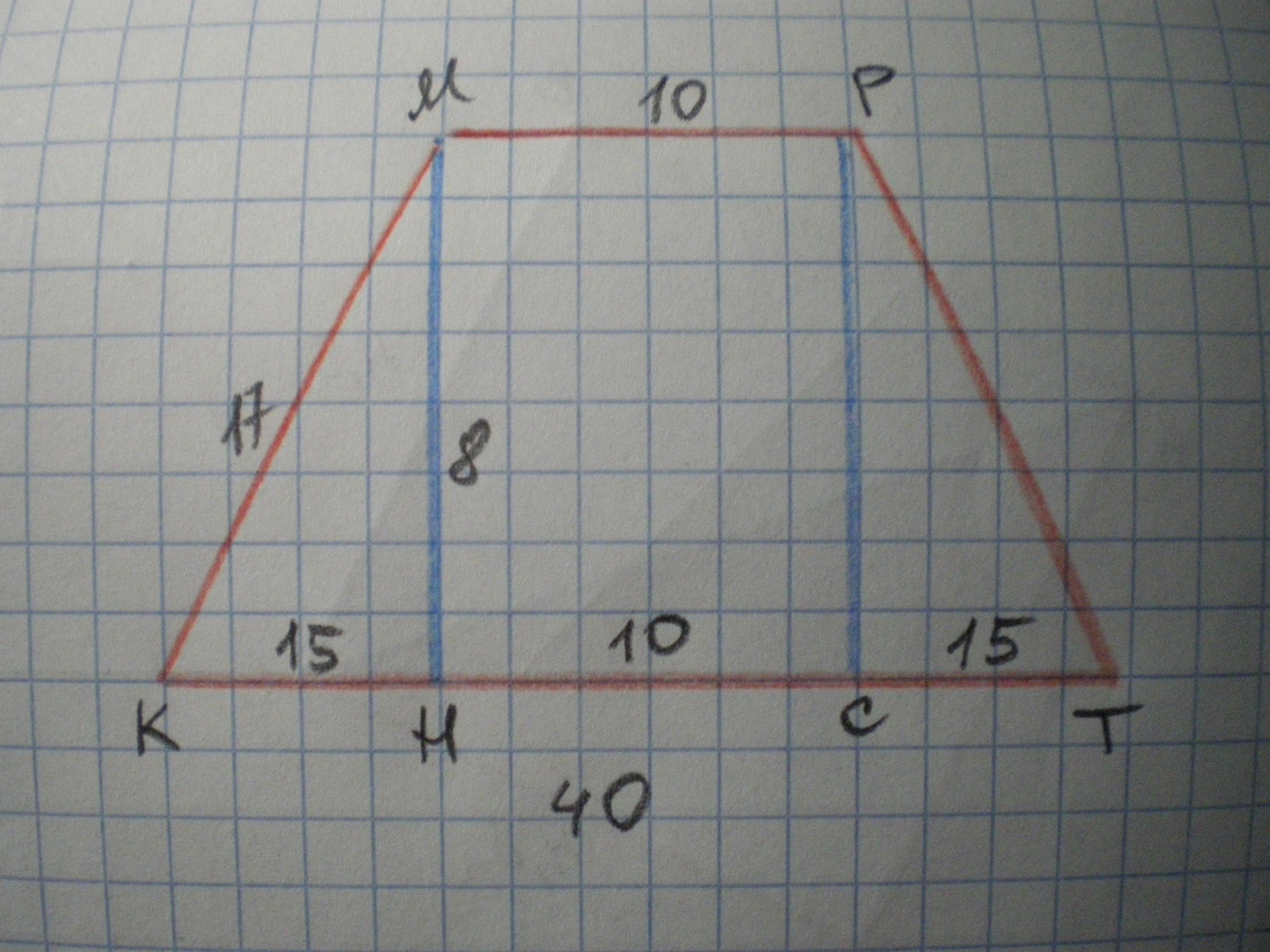
Основания равнобедренной трапеции равны 10 и 40, а ее боковые стороны равны 17. Найдите площадь трапеции.

Answer 1

Ответ:

200 см²

Объяснение:

Дано: КМРТ - трапеция, КМ=РТ=17 см. МР=10 см, КТ=40 см. Найти S(КМРТ).

Решение: проведем высоты МН и РС, тогда НС=МР=10 см,

КН=СТ=(40-10)/2=15 см (ΔКМН=ΔРСТ по катету и гипотенузе, т.к. МН=РС и КМ=РТ)

По теореме Пифагора МН=√(КМ²-КН²)=√(289-225)=√64=8 см.

S=(МР+КТ)/2 * МН=(10+40)/2 * 8=200 см²