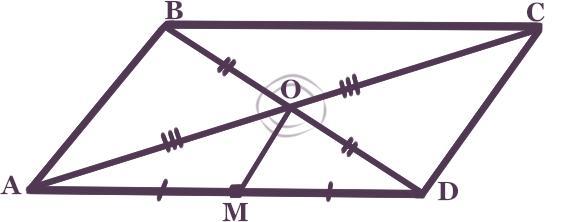
В параллелограмме ABCD точка M -середина стороны AD,О-точка пересечения диагоналей. Докажите,что площадь треугольника AOM в 8 раз меньше площади параллелограмма ABCD
Срочно!
Ответы
Ответ дал:
15
Дано :
Четырёхугольник ABCD - параллелограмм.
Точка М - середина AD.
Отрезки АС и BD - диагонали.
Точка О - точка пересечения диагоналей.
Доказать :
Доказательство :
- Диагонали параллелограмма точкой пересечения делятся пополам.
Следовательно -
BO = OD, AO = OC.
Рассмотрим ΔABD.
Для ΔABD отрезок АО - медиана (по определению).
Сама же S(ΔABD) в два раза меньше S(ABCD) (так как диагональ параллелограмма делит его на два равных треугольника, которые так же имеют равные площади).
То есть -
- Медиана делит треугольник на два равных по площади треугольника.
Отсюда -
S(ΔAOD) = S(ΔABO) = .
Рассмотрим ΔAOD.
Для него отрезок ОМ - медиана (по определению).
Тогда по выше сказанному -
S(ΔAOM) = S(ΔMOD) = .
Ответ :
Что требовалось доказать.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад