Вычислить несобственный интеграл
Помогите пожалуйста срочно!
Приложения:
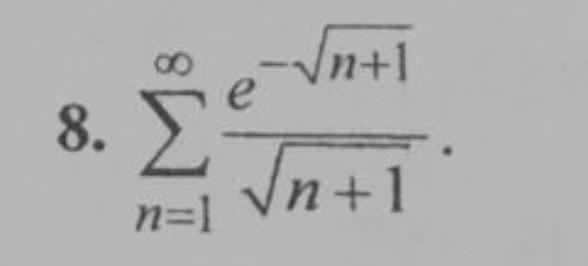
Alexаndr:
Ну и где здесь интеграл?
на фото посмотрите
На фото я вижу ряд.
Ответы
Ответ дал:
1
На будущее: задание формулируйте правильно: Проверить на сходимость интегральным признаком Коши. А то написано вычислите интеграл, на картинке ряд нарисован, и сиди ломай голову.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад