Question

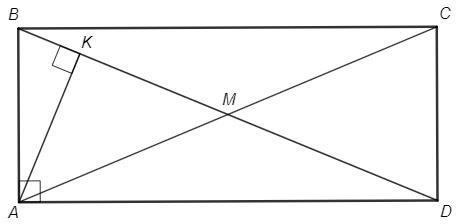
В прямоугольнике ABCD провели перпендикуляр AK к диагонали BD. Угол BAK в 3 раза меньше угла KAD. Докажите, что треугольник AKM – равнобедренный, где M – точка пересечения диагоналей прямоугольника ABCD.

Answer 1

BAK/KAD=1/3 => BAK=90/4

Сумма острых углов прямоугольного треугольника равна 90.

BDA =90-ABD =BAK

Диагонали прямоугольника равны и точкой пересечения делятся пополам.

△AMD - равнобедренный, MAD=BDA

KAM= 90-BAK-MAD =90/2 =45

KMA=90-45=45

KMA=KAM, △AKM - равнобедренный