Предмет: Геометрия
Автор: rozannadzakhmish
Вопрос задан 1 год назад

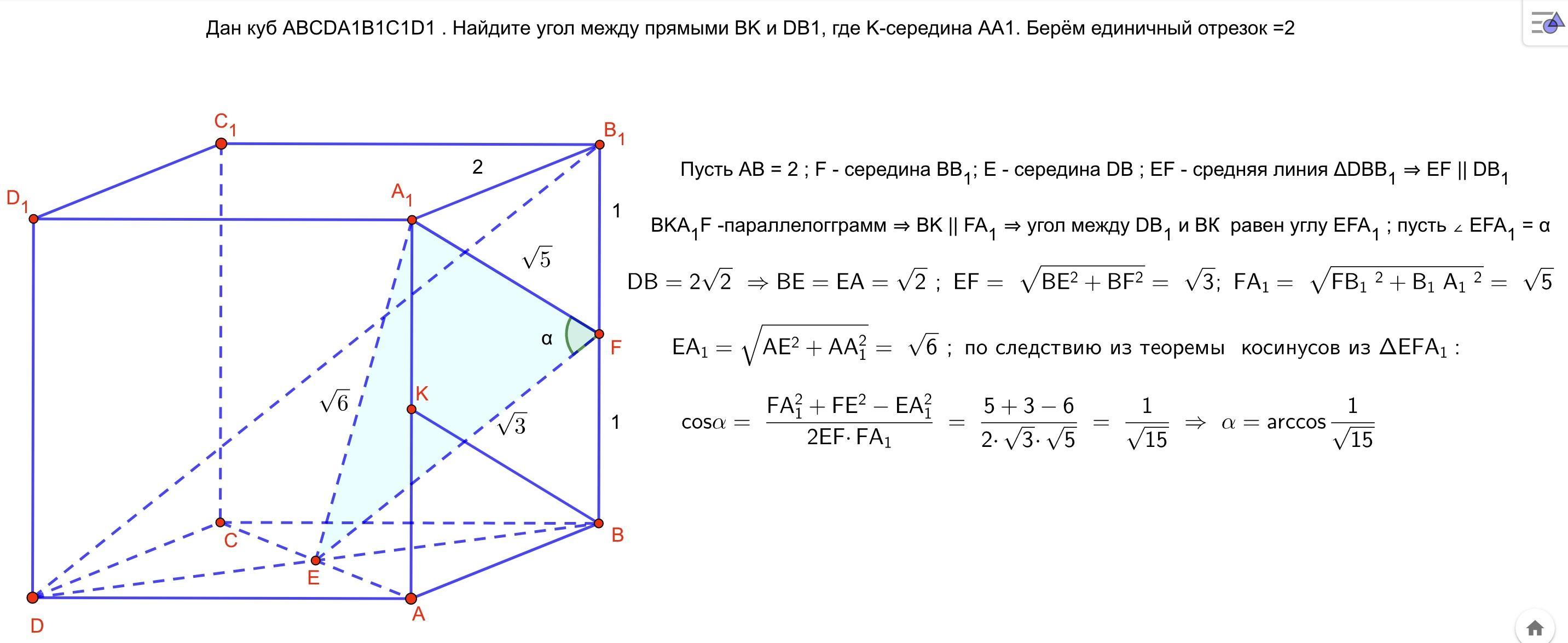
Дан куб ABCDA1B1C1D1 . Найдите угол между прямыми BK и DB1, где K-середина AA1. Берём единичный отрезок =2

Ответы

Ответ дал: antonovm

Решение : //////////////////////////////

Приложения:

ivanproh1: Координатный (векторный) метод.
Дан единичный куб со стороной, равной 2.
Привяжем систему координат к вершине В.
Тогда имеем точки: В(0;0;0;), К(0;2;1),
В1(0;0;2), D(2;2;0).
Вектор ВК{0;2;1} |BK| = √5.
Вектор В1D{2;2;-2} |BK| = 2√3.
Cosα = (0+4-2)/2√15 = 1/√15 = √15/15 ≈ 0,258
α = arccos0,258 ≈ 75°.

Вас заинтересует

Математика

1 год назад

ПОМОГИТЕ СРОЧНО У МЕНЯ МАЛО ВРЕМИНИ Чему равно число составляющее 11/12 от 48/5

Математика

1 год назад

Есть 15 дерево если его разделить на 3 части уйдёт 5мин. Вопрос если 15 дерево разделить на 5 частей сколько времени уйдёт?

Английский язык

1 год назад

4 YOUR OPINIONS Ask and answer the questions. 1 Do you think sustainability is possible? 2 What other things can individuals do to help create an ecological balance? 3 What do you think of the Tamil

Українська література

1 год назад