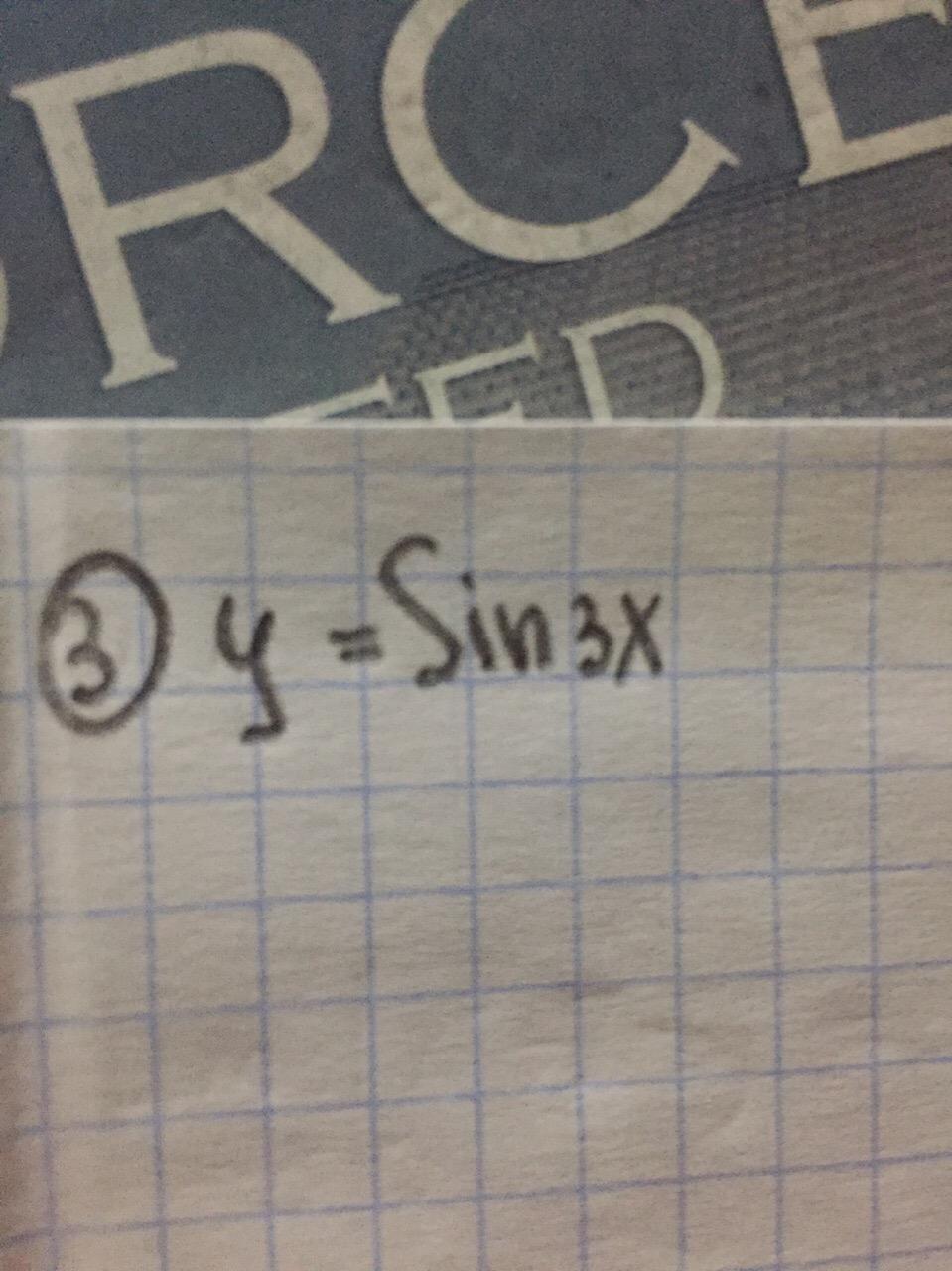Ответы
Ответ дал:
0
Y=(sin3x)’=sin’(3x)*(3x)’=3sin3x
Ответ дал:
1
Ответ:
y'' = -9 sin3x
Пошаговое объяснение:
Производные от функций и от сложной функции:
(sinx)' = cosx
(cosx)' = -sinx
(f(g(x)))'=f'(g(x))·g'(x)
Тогда
y'= (sin3x)'= cos3x · (3x)'= cos3x · 3 = 3·cos3x
y''= (3·cos3x)'= 3·(-sin3x) · (3x)'= -3·sin3x · 3 = -9·sin3x
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад