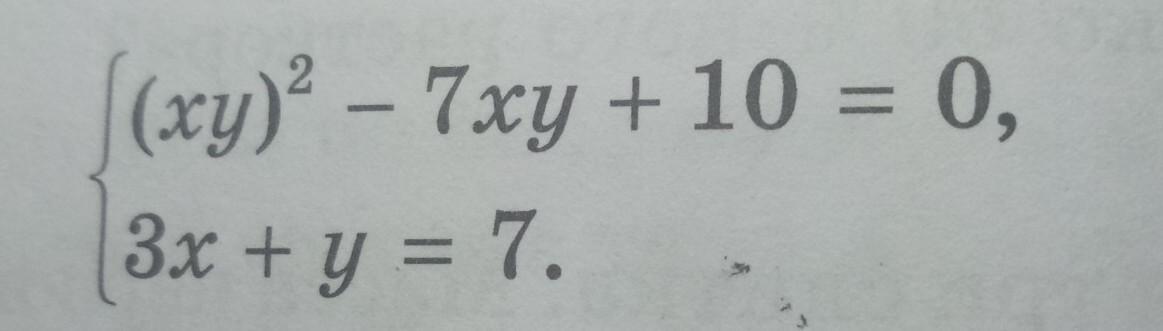Question

Помогите пожалуйста!!!!
Решите МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННЫХ систему уравнений​

Answer 1

Ответ:

х1= 2; у1=1

х2=1/3; у2=6

или

Ответ: (2; 1) и (1/3; 6)

Объяснение:

(xy)^2 - 7xy + 10 = 0

3x + y = 7

Рассмотрим 1 уравнение,

(xy)^2 - 7xy + 10 = 0

заменим ху на t

Получим:

t^2 - 7t + 10 = 0

D= 7^2 - 4•10 = 49-40=9>0

t1= (7+√9)/2= 10/2=5

t2= (7-√9)/2 = 4/2=2

Два корня дают 2 системы:

1)

ху=5

3х+у=7 <=> у=7-3х

2)

ху=2

3х+у=7 <=> у=7-3х

решим 1).

ху=5

у=7-3х

Заменим в верхнем уравнении

у на 7-3х:

х(7-3х)=5

7х - 3х^2 - 5 = 0

3х^2 - 7х + 5 = 0

D = 7^2 - 4•3•5= 49-60=-11<0

Корней нет.

Решим 2):

ху=2

у=7-3х

Заменим в верхнем уравнении

у на 7-3х:

х(7-3х)=2

7х - 3х^2 - 2 = 0

3х^2 - 7х + 2 = 0

D = 7^2 - 4•3•2= 49-24=25 > 0

х1 = (7+√(25))/(2•3) = 12/6 = 2

у1 = 7-3х= 7-3•2= 7-6=1

х2= (7-√(25))/(2•3)= 2/6= 1/3

у2 = 7-3х = 7 - (3•1/3)=6

Ответ:

х1= 2; у1=1

х2=1/3; у2=6