Question

Помогите с геометрией
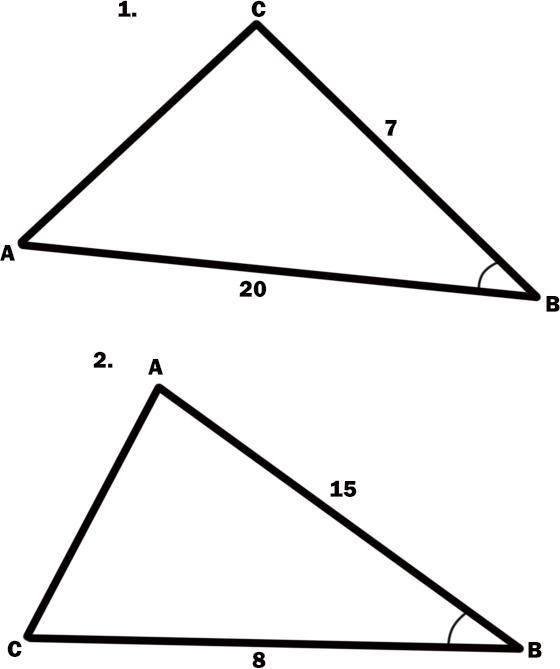
1)В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника
2)треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.

​

Answer 1

№1.

Дано :

ΔАВС.

АВ = 20.

ВС = 7.

Sin(∠ABC) = 2/5.

Найти :

S(ΔАВС) = ?

Решение :

• Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.

В нашем случае -

S(ΔABC) = 0,5*АВ*ВС*sin(∠ABC)

S(ΔABC) = 0,5*20*7*(2/5)

S(ΔABC) = 70*(2/5)

S(ΔABC) = 140/5

S(ΔABC) = 28 (ед²).

Ответ :

28 (ед²).

№2.

Дано :

ΔАВС.

АВ = 15.

ВС = 8.

Sin(∠ABC) = 5/6.

Найти :

S(ΔАВС) = ?

Решение :

• Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.

Соответственно -

S(ΔABC) = 0,5*BC*АВ*sin(∠ABC)

S(ΔABC) = 0,5*8*15*(5/6)

S(ΔABC) = 60*(5/6)

S(ΔABC) = 300/6

S(ΔABC) = 50 (ед²).

Ответ :

50 (ед²).