Ответы
Ответ дал:
2
Ответ:
В фото
Объяснение:
Используем метод замены переменных
Приложения:
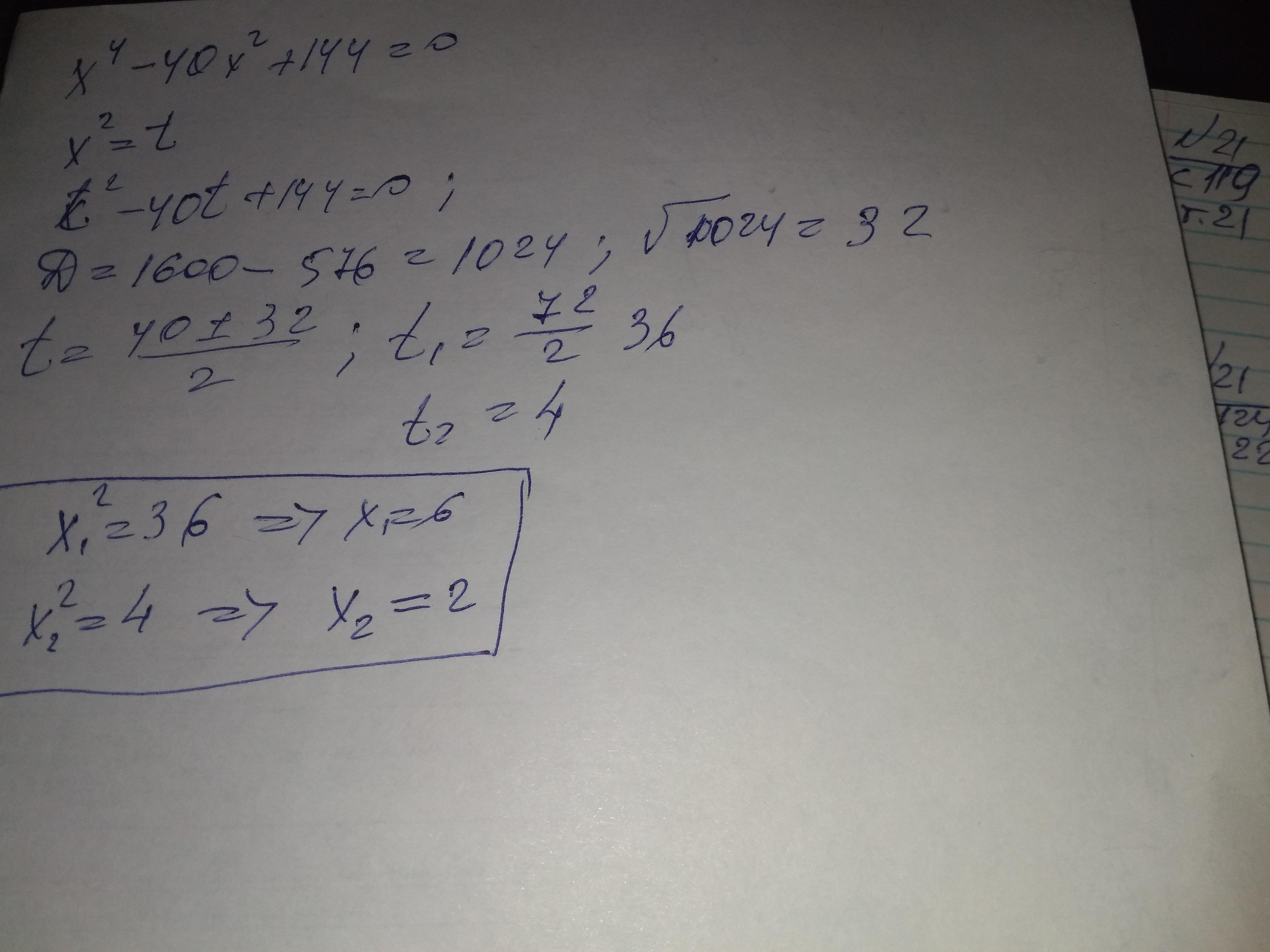
Ответ дал:
0
Объяснение:
Пусть t=x^2
Тогда t^2-40t+144=0
D=1600-576=1024
D=32
t1=
t2=
x1=
x2=
Ответ:x=6 и x=2
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
