Question

решить систему уравнений​

Answer 1

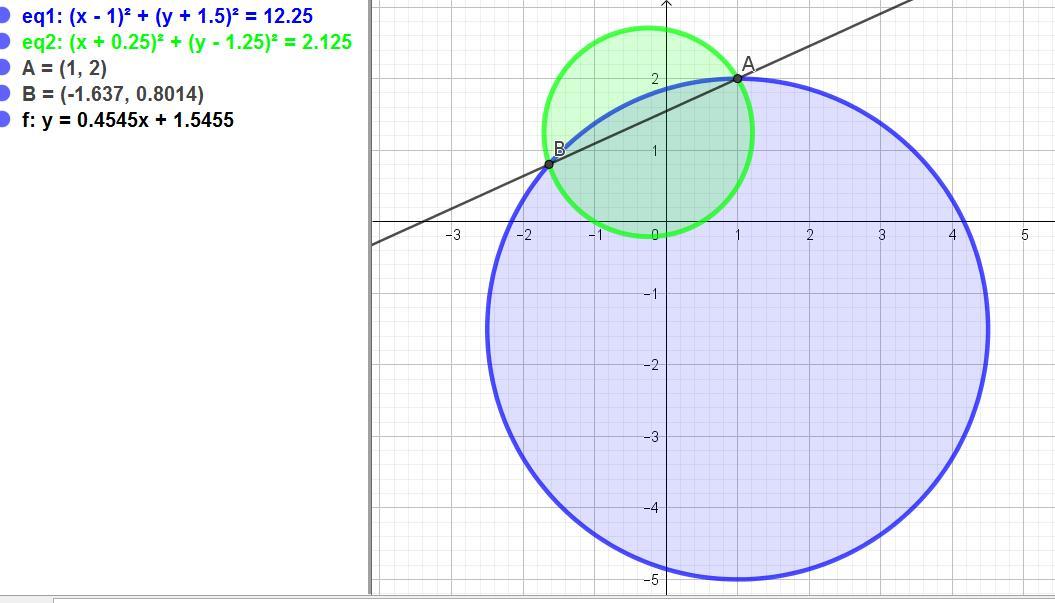
Заданные уравнения представляют собой уравнения окружностей.

Это становится ясным, если выделить полные квадраты:

(x - 1)² + (y + 1,5)² = 12,25  

(x + (1/4))² + (y - (5/4))² = 2,125.

Для решения системы первое уравнение умножим на 2:

2x² + 2y² - 4x + 6y = 18,

2x² + 2y² + x - 5y = 1.    Вычтем из второго уравнения первое.

5x - 11y = -17.

Используем метод замены переменной: y = (5/11)x + (17/11).

Если подставим это значение в любое из заданных уравнений, то получим уравнение с одной переменной.

Получится квадратное уравнение, решив которое находим 2 точки пересечения окружностей, которые и являются решением системы.

Точка А(1; 2), точка В((-239/146); (117/146)).