Question

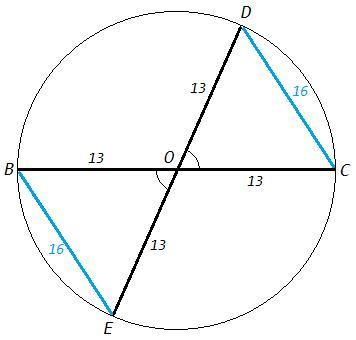
BC и DE - диаметры окружности с центром в точки О.
Найти : P : COD ; BC = 26 см, BE =16
Если можно пожалуйста приложить рисунок. Срочно помогите пожалуйста ​

Answer 1

OB=OC=OD=OE =26/2 =13 (радиусы)

∠BOE=∠COD (вертикальные углы)

△BOE=△COD (по двум сторонам и углу между ними)

BE=CD =16

P(COD)= OC+OD+CD =13+13+16 =42 (см)