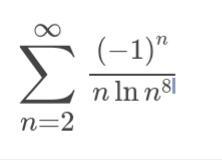Question

Исследовать ряд на сходимость

Answer 1

Ответ: ряд сходится.

Объяснение:

Благодаря наличию множителя (-1)^n данный ряд является знакочередующимся. Модуль его n-го члена /an/=1/[8*n*ln(n)], а модуль его n+1 - го члена /an+1/=1/[8*(n+1)*ln(n+1)]. Так как при любом значении n /an+1/:/an/=n*ln(n)/[(n+1)*ln(n+1)]<1,  то члены данного ряда монотонно убывают по модулю. А так как при этом, очевидно, an⇒0 при n⇒∞, то отсюда - по признаку Лейбница - ряд сходится.