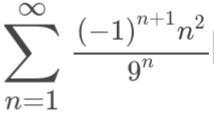Ответы
Ответ дал:
1
1) Ряд знакочередующийся
2)
А значит при монотонно стремится к 0
Тогда ряд сходится по признаку Лейбница
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад