Найдите: первый член и знаменатель геометрической прогрессии, если b3=4, b5=16.
Пожалуйста помогите, используя формулу n-ного члена геометрической прогрессии. Пожалуйста ❤️ даю очень много баллов !!!
Ответы
Ответ дал:
1
Найдём 4-й член. Он равен среднему геометрическому соседних членов (возможно, взятому и со знаком минус, если прогрессия знакочередующаяся):
Рассмотрим два случая.
Первый случай
. Тогда знаменатель равен
. Первый член найдём из формулы 3-го члена:
Второй случай
Ответ:
Ответ дал:
5
Ответ:
Объяснение:
-----------------------------
Приложения:
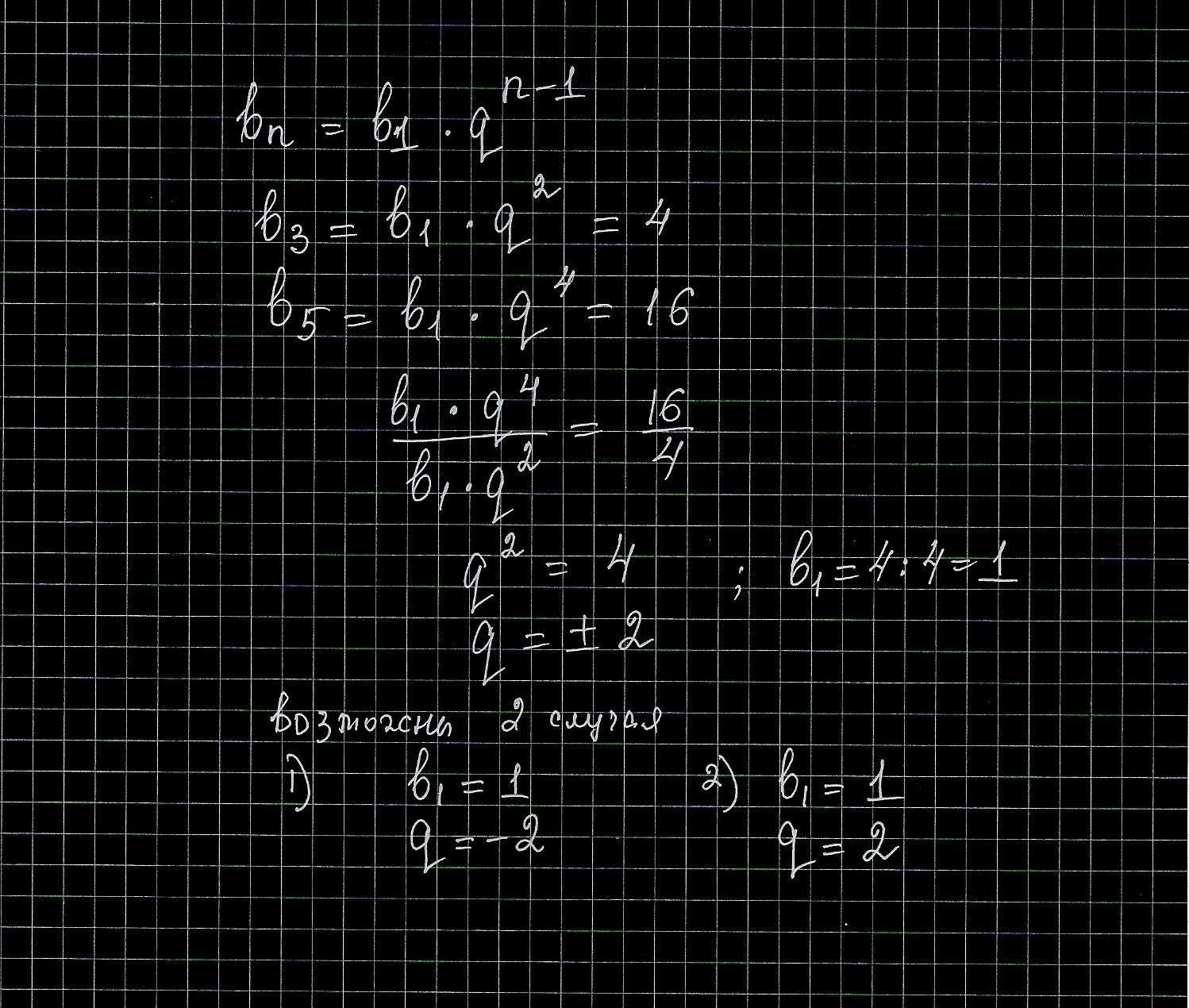
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
9 лет назад