Question

Найти стороны a,b,c​

Answer 1

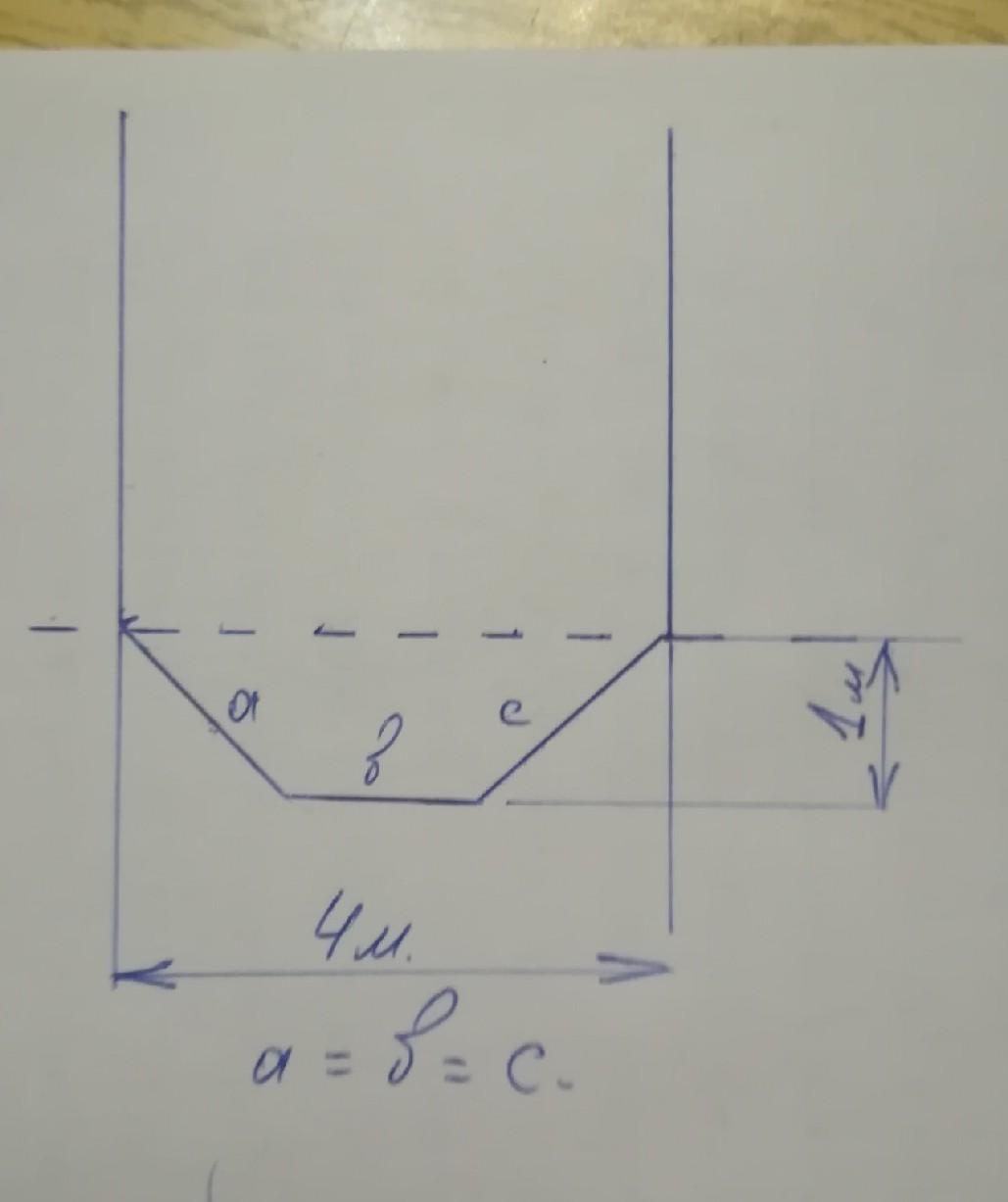
Если стороны a, b и c​ равны между собой, то можно их приравнять а.

Спроецируем эти отрезки на прямую, соединяющую их концы.

Применим формулу Пифагора: √(a² - 1) + a + √(a² - 1) = 4.

2√(a² - 1) = 4 - a. Возведём обе части в квадрат.

4(a² - 1)  = 16 - 8a  + a².  Получаем квадратное уравнение:

3a² + 8a - 20 = 0.

Ищем дискриминант:

D=8^2-4*3*(-20)=64-4*3*(-20)=64-12*(-20)=64-(-12*20)=64-(-240)=64+240=304;

Дискриминант больше 0, уравнение имеет 2 корня:

a_1=(√304-8)/(2*3)=(√304-8)/6=(4√19)/6-(8/6)=(2√19-4)/3 ≈ 1.5726;

a_2=(-√304-8)/(2*3)=(-√304-8)/6=-√304/6-8/6=-√304/6-(4/3)≈-4.2393.

Отрицательный корень отбрасываем.

Ответ: все стороны равны (2√19 - 4)/3 или ≈ 1,5726.