Question

Найти расстояние между фокусами эллипса$\frac{x^2}{16}+\frac{y^2}{25}=1$

Answer 1

$\dfrac{x^2}{4^2}+\dfrac{y^2}{5^2}=1\\\\ \dfrac{x^2}{5^2}+\dfrac{y^2}{4^2}=1$

Здесь параметры a = 5 и b = 4.

Фокусное расстояние и полуоси связаны соотношением:

a² = b² + c²

c² = a² - b² = 5² - 4² = 9

Откуда c = 3

Расстояние между фокусами: 2c = 2 * 3 = 6

Answer 2

Каноническое уравнение, задающее эллипс, выглядит так:

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$

Перепишем уравнение эллипса, поменяв местами параметры $a$ и $b$:

$\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\\\\\dfrac{x^2}{5^2}+\dfrac{y^2}{4^2}=1$

При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.

Найдём эксцентриситет:

$e=\sqrt{1-\dfrac{4^2}{5^2}}=\sqrt{1-\dfrac{16}{25}}=\sqrt{\dfrac{9}{25}}=\dfrac{3}{5}$

Найдём фокальное расстояние (полурасстояние между фокусами):

$c=ae=5 \cdot \dfrac{3}{5}=3$

Тогда расстояние между фокусами в два раза больше: $3 \cdot 2=6$.

Ответ: 6 ед.

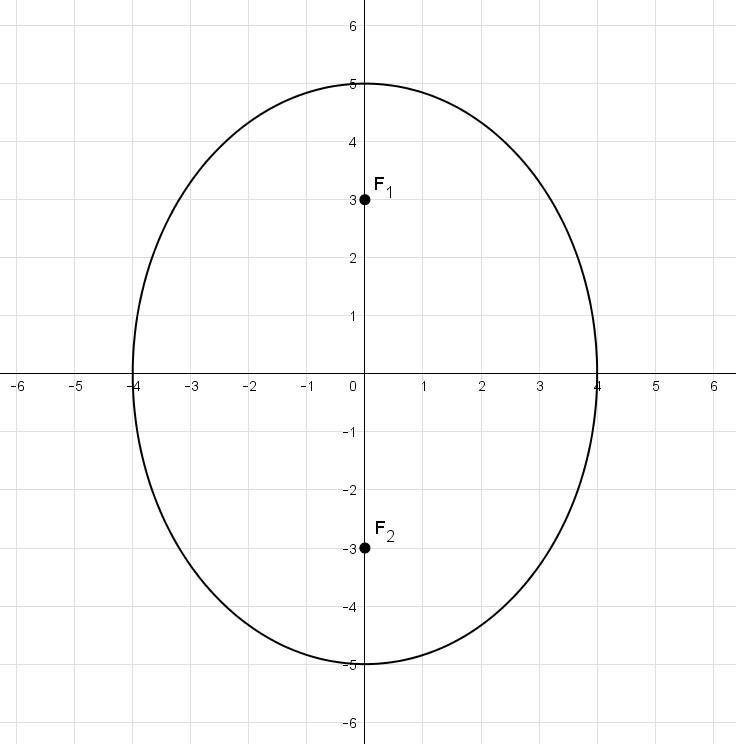
На чертеже изображён данный эллипс. $F_1$ и $F_2$ — его фокусы.