Question

Постройте график функции y=(x-2)²-4. Пользуясь графиком, найдите:
а) область значения функции;
б) промежутки, на которых функция приобретает положительных значений;
в) промежуток, на котором функция растет.

Прошу, если собираетесь отвечать, то с полным объяснением и расписыванием

Answer 1

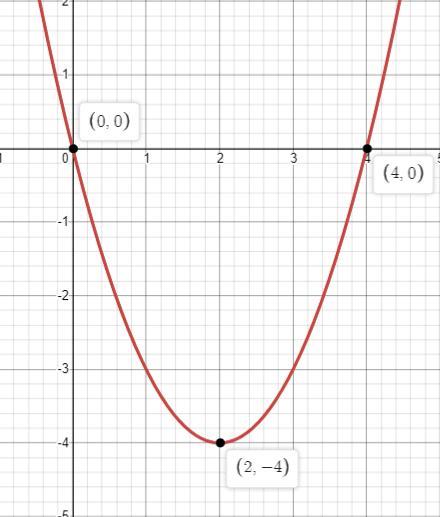
f(x)=(x-2)²-4⇔f(x)=x²-4x

Это парабола ,которую опустили вниз на 4 единицы

Пересечение с Ох:(x-2)²-4=0⇔(x-2-2)(x-2+2)=0⇔(x-4)x=0⇒x={0;4}

Пересечение с Оу:(0-2)²-4=0⇒y=0

Вершина параболы:x₀=-b/2a=4/2=2⇒y₀=(2-2)²-4=-4

Коэффициент а>0 ,следовательно ветви параболы направлены вверх

Вершина нашей параболы - точка минимума

a)Область значения функции: E(f(x))=[-4;+∞)

б)x²-4x>0⇔x(x-4)>0⇒x∈(-∞;0)∪(4;+∞)

в)Найдём производную

f'(x)=2x-4

f'(x)=0⇒2x-4=0⇒x=2

--(-)--(2)--(+)--

На промежутке (-∞;2) - Функция убывает

На промежутке (2;+∞) - Функция возрастает