Question

Помогите решить, пожалуйста
За решение даю 35
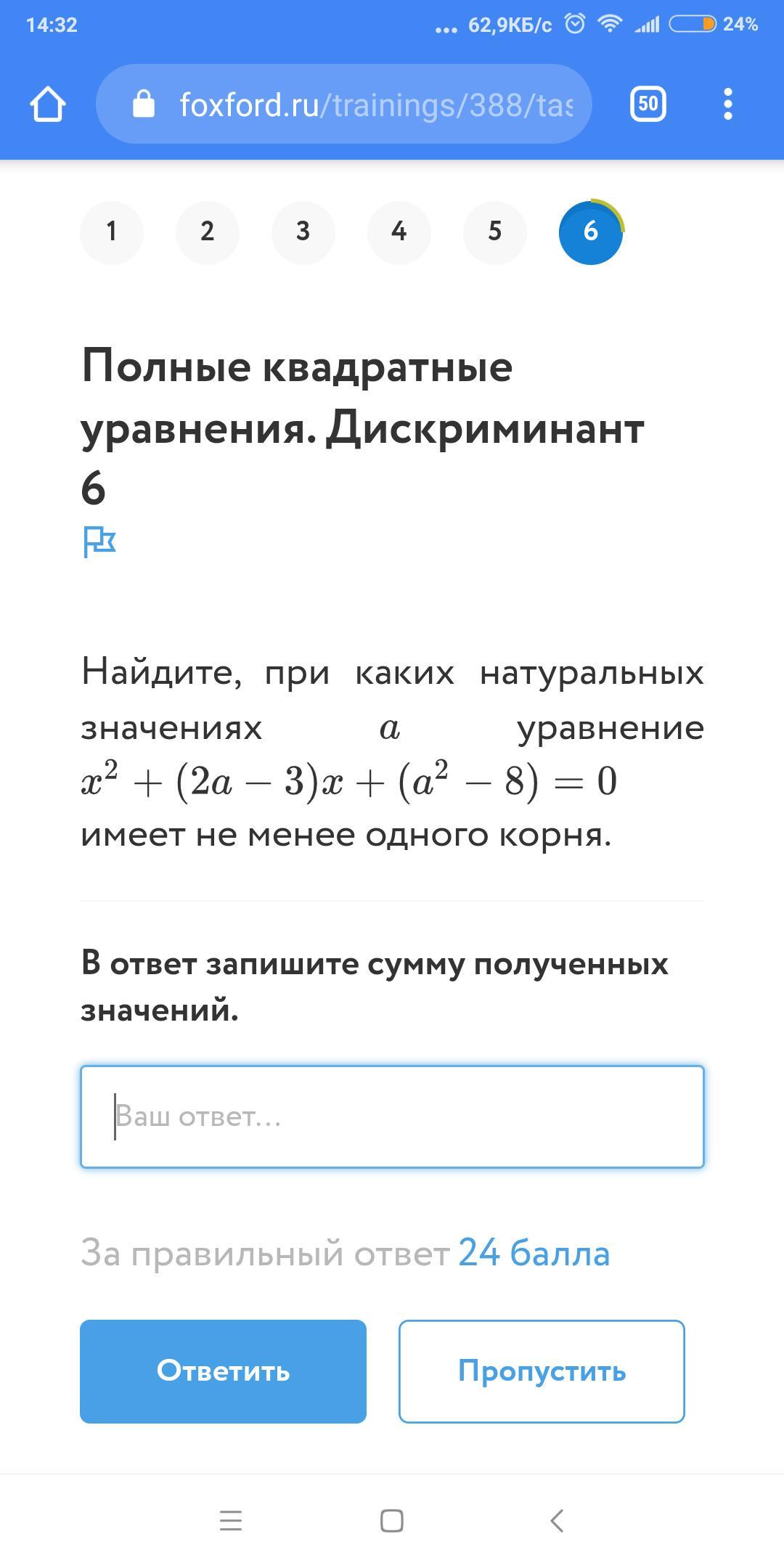
Задание на скриншоте: Найдите при каких натуральных значениях а уравнение x²+(2a-3)x+(a²-8)=0 имеет не менее одного корня

Answer 1

Ответ: 6.

Объяснение: x² + (2a - 3)x + (a² - 8) = 0.

Данное уравнение - квадратное. Квадратное уравнение имеет не менее одного корня, если его дискриминант D ≥ 0.

Найдем дискриминант:

D = b² - 4ac = (2a - 3)² - 4 × 1 × (a² - 8) = 4a² - 12a + 9 - 4a² + 32 = -12a + 41.

Решаем неравенство D≥0:

-12a + 41 ≥ 0;

-12a ≥ -41;

a≤ 41/12.

Натуральное значения параметра а, которые удовлетворяют неравенству - числа 1, 2 и 3.

Сумма данных чисел равна 6.