Найти четыре первых члена (отличных от нуля) разложения в ряд решения дифференциального уравнения
Приложения:
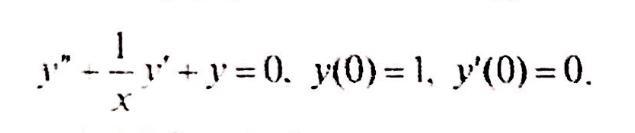
Ответы
Ответ дал:
1
y = a0 + a1 x + a2 x² + a3 x³ + ...
y(0) = a0 = 1
y'(0) = a1 = 0
y'' + y' / x + y =
= (2 a2 + 6 a3 x + 12 a4 x² + 20 a5 x³ + ...) +
+ (2 a2 + 3 a3 x + 4 a4 x² + 5 a5 x³ + ...) +
+ (1 + a2 x² + a3 x³ + ...) = 0
-->
4 a2 + 1 = 0 -> a2 = -1/4
9 a3 = 0 -> a3 = 0
16 a4 + a2 = 0 -> 16 a4 = 1/4 -> a4 = 1/64
25 a5 + a3 = 0 -> a5 = 0
y ≅ 1 - x^2 / 4 + x^4 / 64 + ...
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад