Помогите с Геометрией.
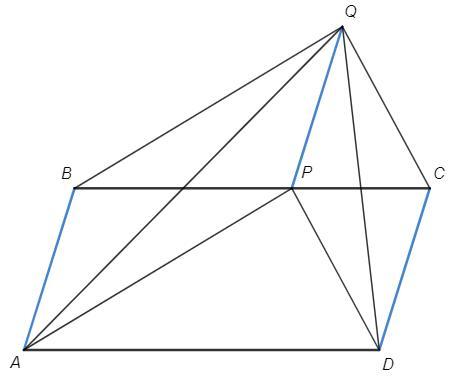
На стороне BC параллелограмма ABCD отмечена точка P, а вне параллелограма - точка Q так, что отрезки BP и AQ имеют общую середину. Докажите, что отрезки CP и DQ имеют общую середину.
Ответы
Ответ дал:
4
Диагонали четырехугольника ABQP точкой пересечения делятся пополам, следовательно ABPQ - параллелограмм. Противоположные стороны параллелограмма (ABQP, ABCD) параллельны и равны,
AB||QP, AB||CD => QP||CD
AB=QP, AB=CD => QP=CD
Противоположные стороны четырехугольника PQCD параллельны и равны, следовательно PQCD - параллелограмм и его диагонали CP и DQ точкой пересечения делятся пополам (то есть имеют общую середину).
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад