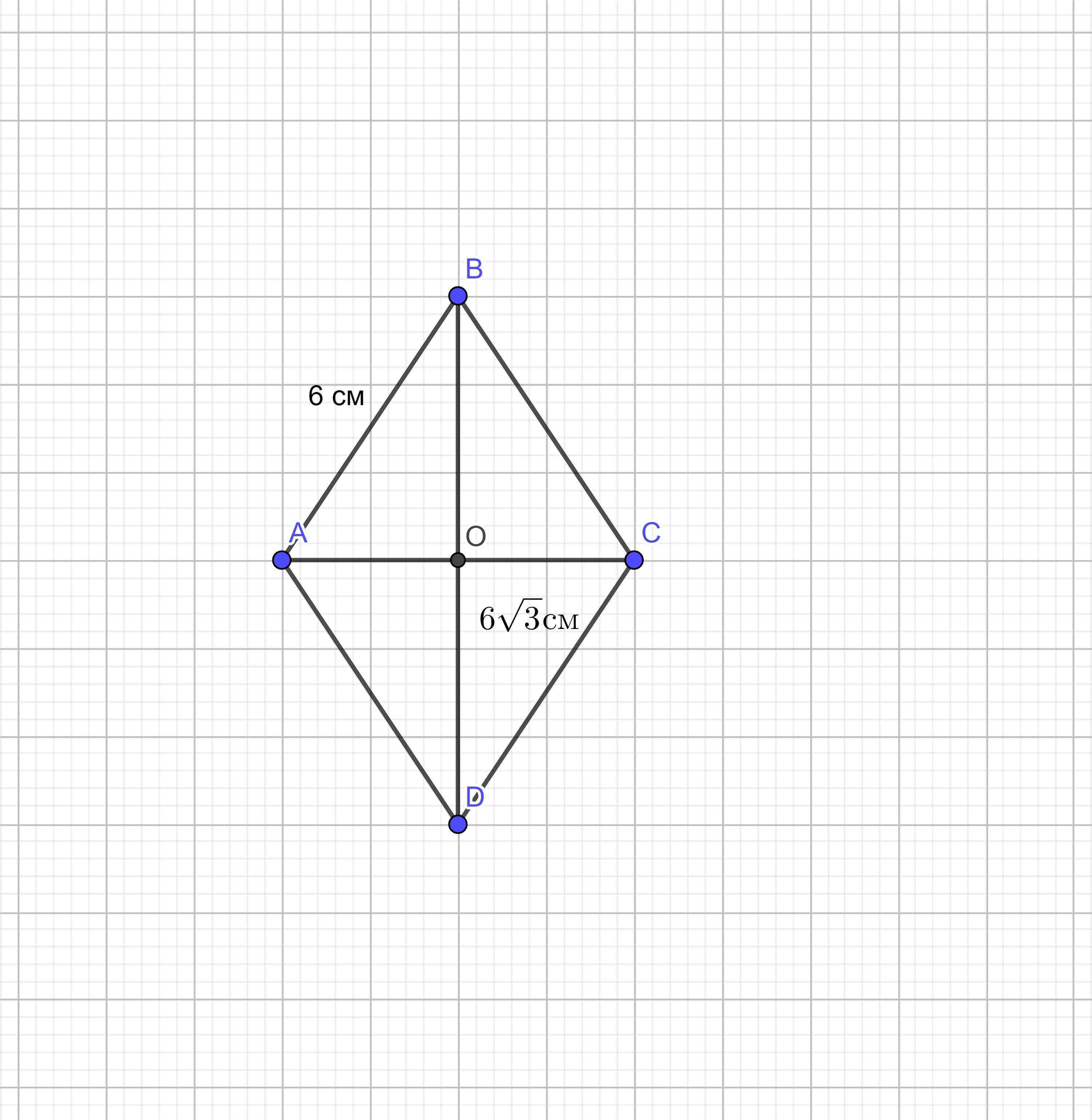
найдите углы ромба ABCD,если его сторона равна 6см, а большая диоганаль 6 под корнем 3
Приложения:

Ответы
Ответ дал:
109
Ответ:
60°, 120°, 60°, 120°.
Объяснение:
В ромбе ABCD AB=6 см и BD= 6√3 см.
Так как диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам, то BO= OD= 6√3:2= 3√3 см и ΔAOB - прямоугольный.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Пусть ∠ABO=α.
Тогда α= 30°, то есть ∠ ABO=30°.
Диагонали ромба являются биссектрисами углов. Значит
∠B= 2*30°=60°.
∠D=∠D= 60° как противолежащие углы ромба.
∠A и ∠B ромба ABCD являются внутренними односторонними при параллельных прямых BC , AD и секущей AB. Их сумма равна 180°.
∠A+∠B=180°
∠A=180°-60°=120°
∠C=∠A =120° как противолежащие углы ромба.
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад