Question

Отрезок AB расположен вне плоскости α по одну сторону от нее. Расстояние от точек A и B до плоскости равны 10 и 14. Найдите расстояние от середины отрезка AB до плоскости α

Answer 1

Ответ:

12

Объяснение:

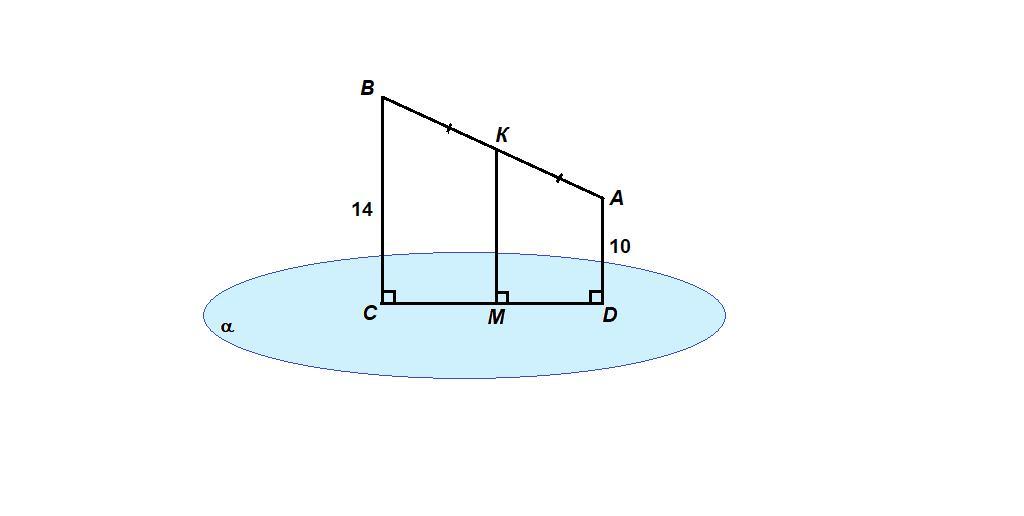
AD⊥α,  BC⊥α, тогда АD║BC как перпендикуляры к одной плоскости,

Через две параллельные прямые проходит единственная плоскость (АВС). Так как отрезок АВ лежит в этой плоскости, то и точка К так же лежит в ней, значит и прямая КМ║ВС, так же лежит в (АВС).

(АВС)∩α = CD, значит М∈CD.

ABCD - прямоугольная трапеция.

К - середина АВ, КМ║ВС (перпендикуляры к одной плоскости), значит

М - середина CD по теореме Фалеса.

КМ - средняя линия трапеции ABCD, значит равна полусумме оснований:

КМ = 1/2 (AD + BC) = 1/2 · (10 + 14) = 12