Помогите, пожалуйста. Дам 50 баллов. Желательно решение, но и просто ответы пойдёт. Спасибо =)
Приложения:
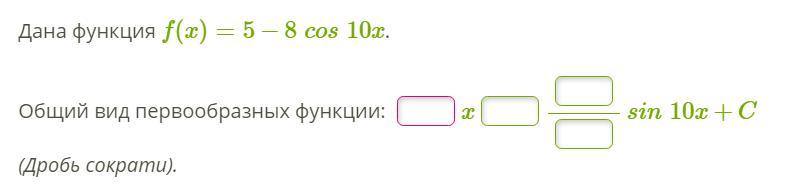

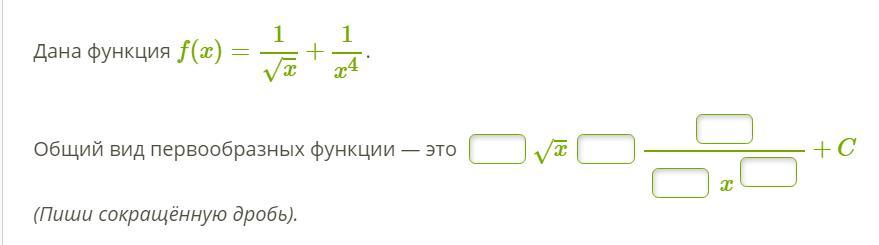
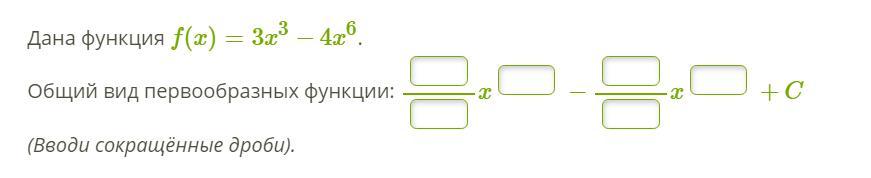
Ответы
Ответ дал:
0
Объяснение:
Общий вид первообразных
Аноним:
А остальные как решать? Если не трудно конечно, объясните =)
Ответ дал:
1
Спасибо Вам, добрый человек)
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад