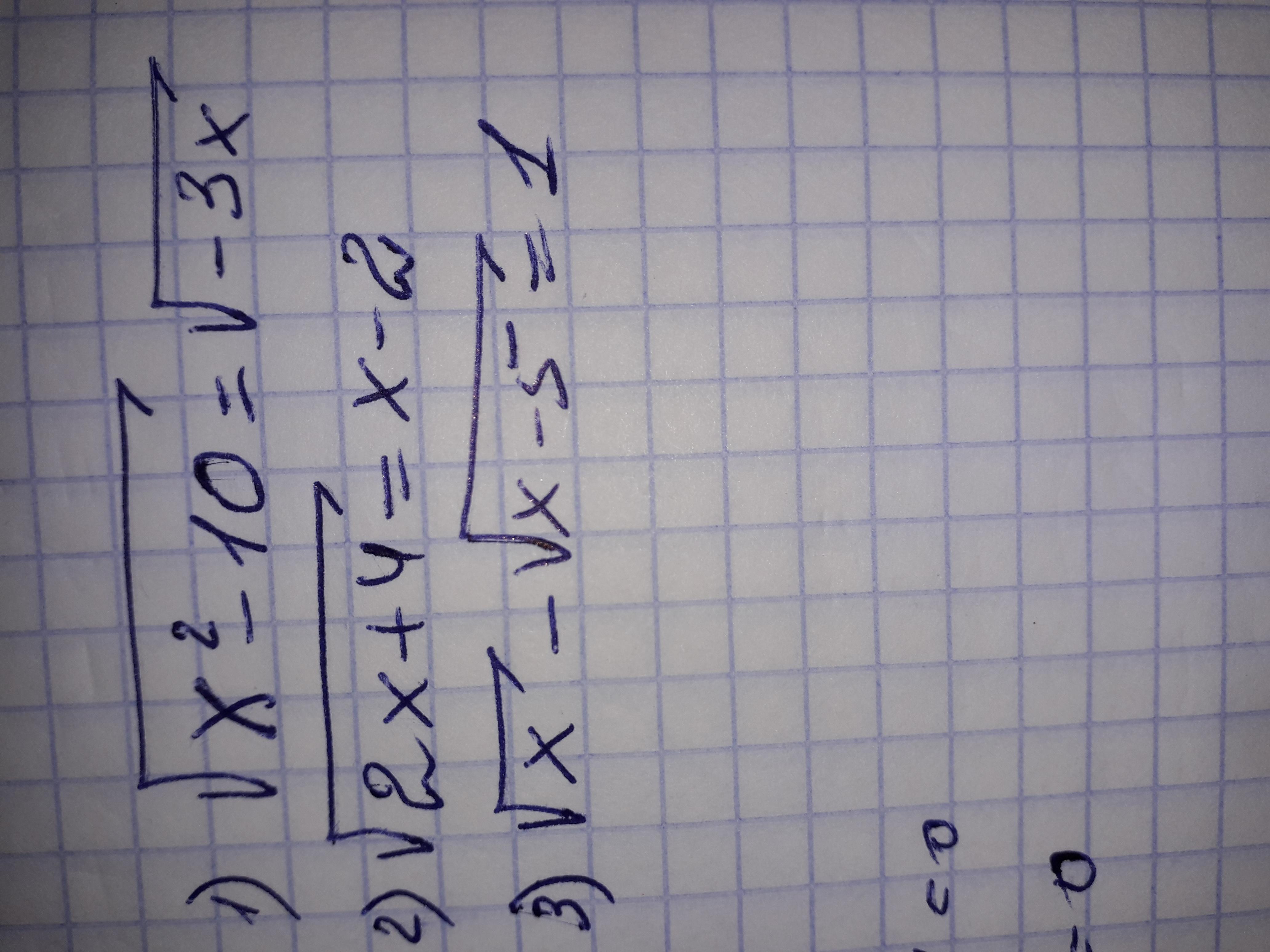Ответы
Ответ дал:
0
При подстановке корня x=2 под квадратным корнем у нас будет отрицательное число, поэтому
ОТВЕТ: X= -5
При подстановке корня x=0 мы имеем: , поэтому
ОТВЕТ: X= 6
Проверкой убеждаемся, что
ОТВЕТ: X= 9
p.s такого вида уравнения нужно решать подносом к квадрату обоих частей, при этом, что бы не появился сторонний корень нужно находить сначала ОДЗ, или как я решал: производить проверку корней. Для этого достаточно подставить найденные корни в начальное уравнение.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад