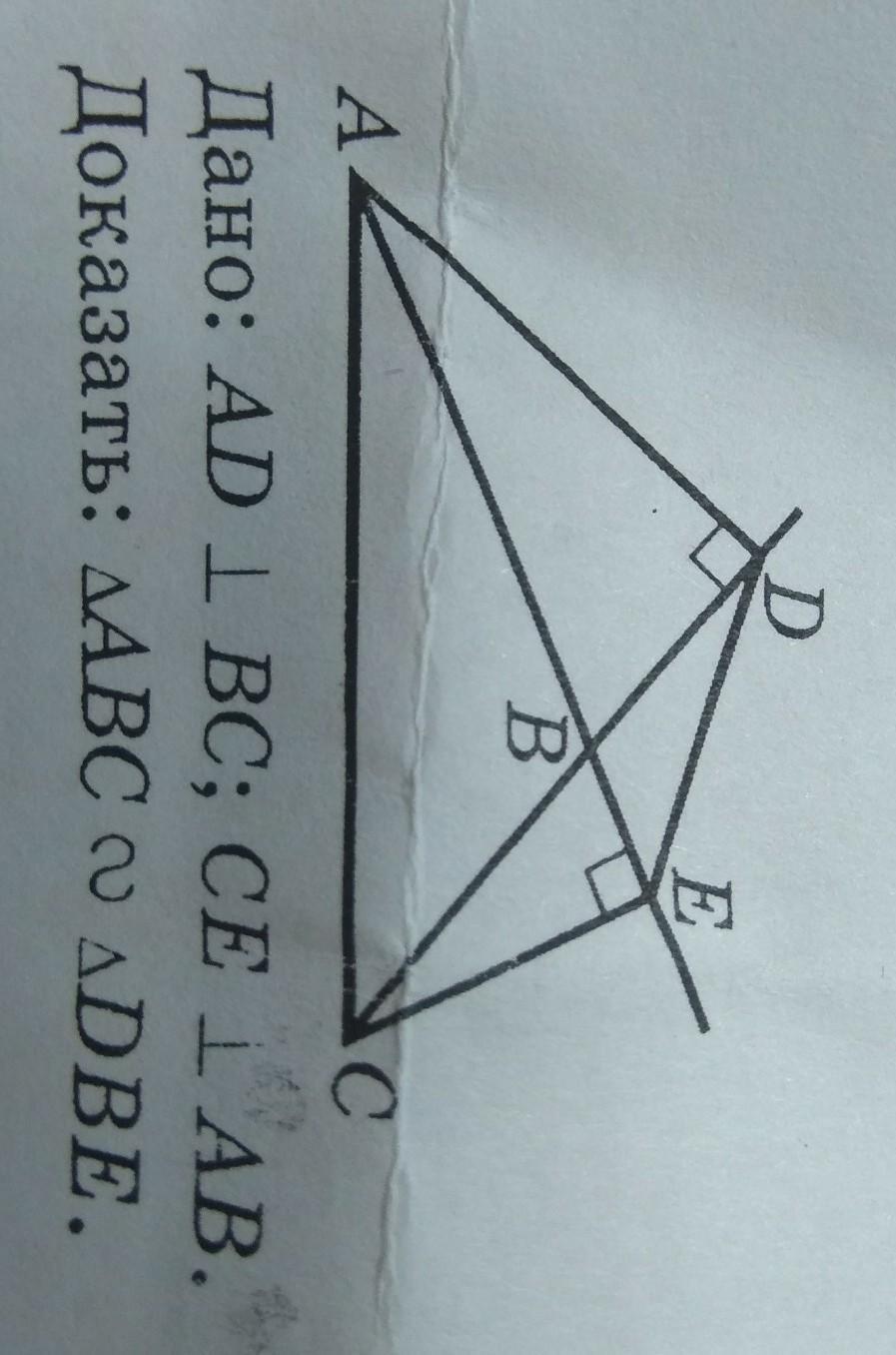
Дано: AD параллельно BC; CE параллельно AB.
Доказать: АВС подобен DBE.
Срочно, пожалуйста
Приложения:
Ответы
Ответ дал:
0
из чертежа понятно, что соответствующие прямые не параллельны а перпендикулярны. Угол ЕВD =АЕС как вертикальные.
Для обоснования подобия достаточно доказать, что равны углы СDЕ и САЕ. Легко заметить, что вокруг четырехугольника АЕСD можно описать окружность с диаметром АС (два прямых угла на АС опираются). Но тогда и углы СDЕ и САЕ . опираются на одну дугу. Значит они равны.
Таким образом в треугольниках ЕВD и АЕС углы ЕВD и АЕС равны как верткальные, а СDЕ и САЕ равны, как это доказано выше, значит треугольники подобны по двум углам.
klever2403:
эм, но мне нужно доказать подобие треуголников
Это и доказано. Треугольники подобны по двум углам.
Дописал для Вас последнее предложение в доказательство.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад