
a = -1, b=2.
Необходимо найти:
1. Значение постоянной А, при котором f(x) будет плотностью распределения некоторой случайной величины Х
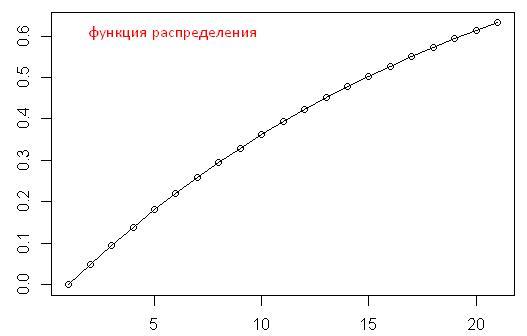
2. Интегральную функцию распределения F(x) этой случайной величины Х.
3. Мат. ожидание, дисперсию, среднее квадрат. отклонение.
4. Вероятность попадания СВ Ч в интервал (а,b).
Построить графики функций F(x) и f(x)
Аноним:
так как изначально задана плотность распределения
а не функция распределения)
Хорошо, сразу лучший ответ поставлю тогда :)
вам решают) он вполне справиться с этой задачей)
Видимо не справился :(
я берусь решать её
Будет замечательно:)
A = 1
F(x) = -e^(-x)
DX = MX = 1
Среднее квадратическое отклонение: 1
P(-1 < X < 2) = 1 - exp(-2) = 0.86
F(x) = -e^(-x)
DX = MX = 1
Среднее квадратическое отклонение: 1
P(-1 < X < 2) = 1 - exp(-2) = 0.86
F(x) = 1 - e^(-x)
Подсказка: это показательное распределение
Ответы
Ответ дал:
1
Решение на фотографиях. Приятно удивлен увидеть здесь университетскую жизнь (теорвер). Если что, как берется неопределенный интеграл от xe^-x или x^2 * e^-x опущено, т.к. это легко делается с помощью интегрирования по частям (в первом случае применяем единожды, во втором два раза). Графики можно начертить здесь www.desmos.com/calculator
Приложения:

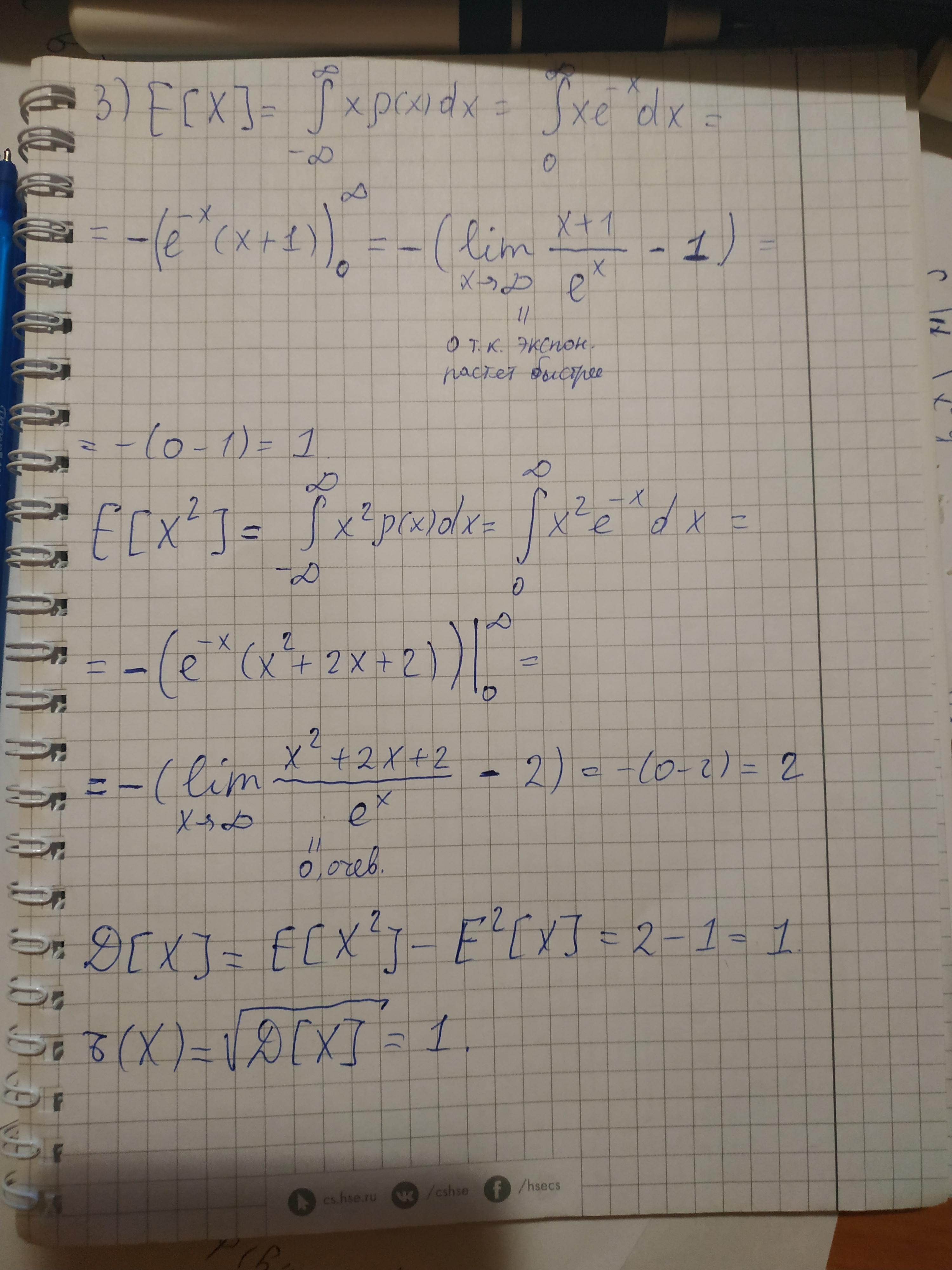

Графиков нет
я уже высказался насчёт графиков. Не вижу смысла ручками рисовать графики и выкладывать сюда
так что дано в условии, плотность распределения или функция распределения?! Если функция, то она немного не так выглядит. F(x) = 1 - e^(-x) .
в условии дана плотность
надо закончить четвертое Вам, графики несложные.
Ответ дал:
2
1)
Воспользовавшись одним из свойств плотности распределения
Заметим, что это показательное распределение с параметром
2)
3) Математическое ожидание случ. величины X:
Дисперсия случ. величины X:
Среднее квадратическое отклонение:
4) Вероятность того, что СВ Х попадет в интервал (-1;2), равна
Приложения:

Вас заинтересует
1 год назад
1 год назад
1 год назад
8 лет назад
8 лет назад