Question

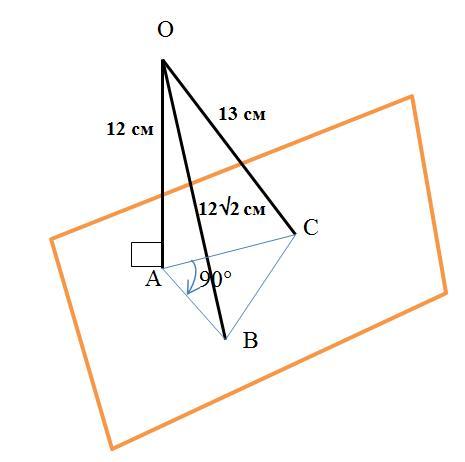
Із точки до площини проведено перпендикуляр довжиною 12$\sqrt{2}$ см i двi похилi, довжини яких дорiвнюють 12square root of 2 см i 13 см. Знайдiть вiдстань мiж основами похилих, якщо кут мiж їх проекцiями дорiвнює 90°

Answer 1

Получили 2 прямоугольных треугольника с одним общим катетом 12 см и гипотенузами 12√2 см и 13 см. Найдем вторые катеты (проекции наклонных).

а1=√(h²-c1²)=√(144*2-144)=√144(2-1)=12 см

а2=√(169-144)=√25=5 см

На плоскости тоже прямоугольный треугольник с катетами 12 и 5 см.

Искомое расстояние - гипотенуза=√(144+25)=√169=13 см - это ответ.

Answer 2

Ответ:

13 см

Пошаговое объяснение:

Пусть перпендикуляр, опушенная из точки О пересекает плоскость α в точке А, а наклонные пересекают в точках В и С (см. рисунок). По условию их длины равны: ОА=12 см, ОВ=12√2 см и ОС=13 см.

Так как ОА перпендикуляр, опушенная из точки О к плоскости α, то имеем:

1) проекциями наклонных ОВ и ОС будут АВ и АС;

2) ∠ОАВ=90°, ∠ОАС=90°.

Поэтому по теореме Пифагора, в прямоугольном треугольнике ОАВ: ОВ²=ОА²+АВ², а в прямоугольном треугольнике ОАС: ОС²=ОА²+АС².

Тогда

АВ²=ОВ²-ОА²=(12√2)²-12²=144·2-144=144=12² или АВ=12 см

АС²=ОС²-ОА²=13²-12²=169-144=25= 5² или АС=5 см

Но, по условию, треугольник АВС также прямоугольный. В силу теоремы Пифагора, расстояние между основаниями наклонных находим через катеты АВ и АС:

ВС²=АВ²+АС²=(12 см)² + (5 см)²=144 см² + 25 см² = 169 см²

или ВС= 13 см.