Question

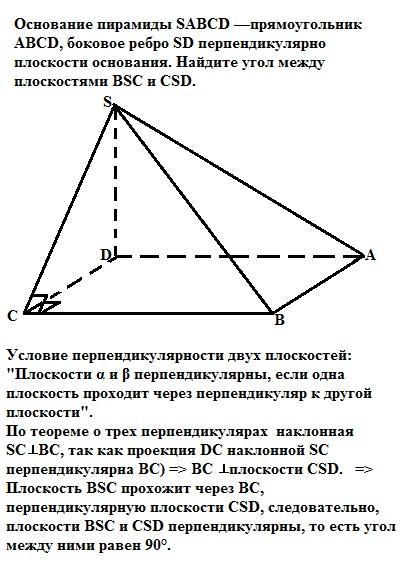
Основание пирамиды SABCD —прямоугольник ABCD, боковое ребро SD перпендикулярно плоскости основания. Найдите угол между плоскостями BSC и CSD.

Answer 1

Ответ:

Угол между плоскостями BSC и CSD равен 90°.

Объяснение:

Условие перпендикулярности двух плоскостей: "Плоскости α и β перпендикулярны, если одна плоскость проходит через перпендикуляр к другой плоскости".

По теореме о трех перпендикулярах  наклонная SC⊥BC, так как проекция DC наклонной SC перпендикулярна ВС (DC и ВС - пересекающиеся стороны прямоугольника) =>

Прямая ВС перпендикулярна плоскости CSD, так как она перпендикулярна двум пересекающимся прямым (DC и SС), лежащим в этой плоскости.

Плоскость BSC проходит через ВС, перпендикулярную плоскости CSD, следовательно, плоскости BSC и CSD перпендикулярны, то есть угол между ними равен 90°.